Область определения функции с корнем

Функция с квадратным корнем определена только при тех значениях «икс», когда подкоренное выражение неотрицательно: . Если корень расположился в знаменателе , то условие очевидным образом ужесточается: . Аналогичные выкладки справедливы для любого корня положительной чётной степени: , правда, корень уже 4-ой степени в исследованиях функций не припоминаю.

Пример 5

Найти область определения функции

Решение: подкоренное выражение должно быть неотрицательным:

Прежде чем продолжить решение, напомню основные правила работы с неравенствами, известные ещё со школы.

Обращаю особое внимание! Сейчас рассматриваются неравенства с одной переменной – то есть для нас существует только одна размерность по оси. Пожалуйста, не путайте с неравенствами двух переменных, где геометрически задействована вся координатная плоскость. Однако есть и приятные совпадения! Итак, для неравенства равносильны следующие преобразования:

1) Слагаемые можно переносить из части в часть со сменой знака.

2) Обе части неравенства можно умножить на положительное число.

3) Если обе части неравенства умножить на отрицательное число, то необходимо сменить знак самого неравенства. Например, если было «больше», то станет «меньше»; если было «меньше либо равно», то станет «больше либо равно».

В неравенстве перенесём «тройку» в правую часть со сменой знака (правило №1):

Умножим обе части неравенства на –1 (правило №3):

Умножим обе части неравенства на (правило №2):

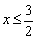
Ответ: область определения:

Ответ также можно записать эквивалентной фразой: «функция определена при ».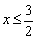
Геометрически область определения изображается штриховкой соответствующих интервалов на оси абсцисс. В данном случае:

Ещё раз напоминаю геометрический смысл области определения – график функции существует только на заштрихованном участке и отсутствует при .

В большинстве случаев годится чисто аналитическое нахождение области определения, но когда функция сильно заморочена, следует чертить ось и делать пометки.

Пример 6

Найти область определения функции

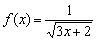
Это пример для самостоятельного решения.

Когда под квадратным корнем находится квадратный двучлен или трёхчлен, ситуация немного усложняется, и сейчас мы подробно разберём технику решения:

Пример 7

Найти область определения функции

Решение: подкоренное выражение должно быть строго положительным, то есть нам необходимо решить неравенство . На первом шаге пытаемся разложить квадратный трёхчлен на множители:

Дискриминант положителен, ищем корни:

Таким образом, парабола пересекает ось абсцисс в двух точках, а это значит, что часть параболы расположена ниже оси (неравенство ), а часть параболы – выше оси (нужное нам неравенство ).

Поскольку коэффициент , то ветви параболы смотрят вверх. Из вышесказанного следует, что на интервалах 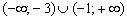выполнено неравенство (ветки параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке 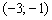ниже оси абсцисс, что соответствует неравенству :

! Примечание:если вам не до конца понятны объяснения, пожалуйста, начертите вторую ось и параболу целиком! Целесообразно вернуться к статье Графики и свойства элементарных функций и методичке Горячие формулы школьного курса математики.

Обратите внимание, что сами точки выколоты (не входят в решение), поскольку неравенство у нас строгое.

Ответ: область определения:

Вообще, многие неравенства (в том числе рассмотренное) решаются универсальным методом интервалов, известным опять же из школьной программы. Но в случаях квадратных дву- и трёхчленов, на мой взгляд, гораздо удобнее и быстрее проанализировать расположение параболы относительно оси . А основной способ – метод интервалов мы детально разберём в статье Нули функции. Интервалы знакопостоянства.

Пример 8

Найти область определения функции

Это пример для самостоятельного решения. В образце подробно закомментирована логика рассуждений + второй способ решения и ещё одно важное преобразование неравенства, без знания которого студент будет хромать на одну ногу…, …хмм… на счёт ноги, пожалуй, погорячился, скорее – на один палец. Большой палец.

Может ли функция с квадратным корнем быть определена на всей числовой прямой? Конечно. Знакомые всё лица: . Или аналогичная сумма с экспонентой: . Действительно, для любых значения «икс» и «ка»: 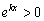, поэтому подАвно и .

А вот менее очевидный пример: . Здесь дискриминант отрицателен (парабола не пересекает ось абсцисс), при этом ветви параболы направлены вверх, следовательно, и область определения: .

Вопрос противоположный: может ли область определения функции быть пустой? Да, и сразу напрашивается примитивный пример , где подкоренное выражение отрицательно при любом значении «икс», и область определения: (значок пустого множества). Такая функция не определена вообще (разумеется, график тоже иллюзорен).

С нечётными корнями и т.д. всё обстоит гораздо лучше – тут подкоренное выражение может быть и отрицательным. Например, функция определена на всей числовой прямой. Однако у функции единственная точка всё же не входит в область определения, поскольку обращают знаменатель в ноль. По той же причине для функции исключаются точки .

Некоторым посетителям сайта рассматриваемые примеры покажутся элементарными и примитивными, но в этом нет случайности – во-первых, я стараюсь «заточить» материал для нубов, а во-вторых, подбираю реалистичные вещи под конкретные задачи: полное исследование функции, нахождение области определения функции двух переменных и некоторые другие. Всё в математике цепляется друг за дружку.Хотя любители трудностей тоже не останутся обделёнными, более солидные задания встретятся и здесь, и на уроке о методе интервалов.