Область определения функции с логарифмом

Третья распространённая функция – логарифм. В качестве образца я буду рисовать натуральный логарифм, который попадается примерно в 99 примерах из 100. Если некоторая функция содержит логарифм , то в её область определения должны входить только те значения «икс», которые удовлетворяют неравенству . Если логарифм находится в знаменателе: , то дополнительно накладывается условие (так как ).

Пример 9

Найти область определения функции

Решение: в соответствии с вышесказанным составим и решим систему:

Графическое решение для чайников:

Ответ: область определения:

Остановлюсь ещё на одном техническом моменте – у меня ведь не указан масштаб и не проставлены деления по оси. Возникает вопрос: как выполнять подобные чертежи в тетради на клетчатой бумаге? Отмерять ли расстояние между точками по клеточкам строго по масштабу? Каноничнее и строже, конечно, масштабировать, но вполне допустим и схематический чертёж, принципиально отражающий ситуацию.

Пример 10

Найти область определения функции

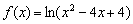
Для решения задачи можно использовать метод предыдущего параграфа – проанализировать, как парабола расположена относительно оси абсцисс. Ответ в конце урока.

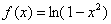Как видите, в царстве логарифмов всё очень похоже на ситуацию с квадратным корнем: функция (квадратный трёхчлен из Примера №7) определена на интервалах , а функция (квадратный двучлен из Примера №6) на интервале . Неловко уже и говорить, функции типа определены на всей числовой прямой.

Полезная информация: интересна типовая функция , она определена на всей числовой прямой кроме точки . Согласно свойству логарифма , «двойку» можно вынести множителем за пределы логарифма, но, чтобы функция не изменилась, «икс» необходимо заключить под знак модуля: . Вот вам и ещё одно «практическое применение» модуля = ). Так необходимо поступать в большинстве случаев, когда вы снОсите чётную степень, например: . Если же основание степени заведомо положительно, например, , то в знаке модуля отпадает необходимость и достаточно обойтись круглыми скобками: .

Чтобы не повторяться, давайте усложним задание:

Пример 11

Найти область определения функции

Решение: в данной функции у нас присутствует и корень и логарифм.

Подкоренное выражение должно быть неотрицательным: , а выражение под знаком логарифма – строго положительным: 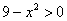. Таким образом, необходимо решить систему:

Многие из вас прекрасно знают или интуитивно догадываются, что решение системы должно удовлетворять каждому условию.

Исследуя расположение параболы относительно оси , приходим к выводу, что неравенству удовлетворяет интервал (синяя штриховка):

Неравенству , очевидно, соответствует «красный» полуинтервал .

Поскольку оба условия должны выполняться одновременно, то решением системы является пересечение данных интервалов. «Общие интересы» соблюдены на полуинтервале .

Ответ: область определения:

Типовое неравенство , как демонстрировалось в Примере №8, нетрудно разрешить и аналитически.

Найденная область определения не изменится для «похожих функций», например, для или . Также можно добавить какие-нибудь непрерывные на функции, например: , или так: , или даже так: . Как говорится, корень и логарифм – вещь упрямая. Единственное, если одну из функций «сбросить» в знаменатель, то область определения изменится (хотя в общем случае это не всегда справедливо). Ну а в теории матана по поводу этого словесного… ой… существуют теоремы.

Пример 12

Найти область определения функции

Это пример для самостоятельного решения. Использование чертежа вполне уместно, так как функция не самая простая.

Ещё пару примеров для закрепления материала:

Пример 13

Найти область определения функции

Решение: составим и решим систему:

Все действия уже разобраны по ходу статьи. Изобразим на числовой прямой интервал, соответствующий неравенству и, согласно второму условию, исключим две точки:

Значение 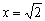оказалось вообще не при делах.

Ответ: область определения

Небольшой математический каламбур на вариацию 13-го примера:

Пример 14

Найти область определения функции

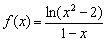
Это пример для самостоятельного решения. Кто пропустил, тот в пролёте ;-)

Завершающий раздел урока посвящен более редким, но тоже «рабочим» функциям: