Области определения функций с тангенсами, котангенсами, арксинусами, арккосинусами

Перед изучением параграфа рекомендую вновь вернуться к первой статье о графиках, чтобы освежить визуальную и аналитическую информацию о перечисленных в заголовке функциях.

Если в некоторую функцию входит , то из её области определения исключаются точки 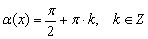, где Z – множество целых чисел. В частности, как отмечалось в статье Графики и свойства элементарных функций, у функции выколоты следующие значения:

То есть, область определения тангенса: .

Убиваться сильно не будем:

Пример 15

Найти область определения функции

Решение: в данном случае и в область определения не войдут следующие точки:

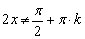
Скинем «двойку» левой части в знаменатель правой части:

В результате :

Ответ: область определения: .

В принципе, ответ можно записать и в виде объединения бесконечного количества интервалов, но конструкция получится весьма громоздкой:

Аналитическое решение полностью согласуется с геометрическим преобразованием графика: если аргумент функции умножить на 2, то её график сожмётся к оси 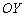в два раза. Заметьте, как у функции уполовинился период, и точки разрыва участились в два раза. Тахикардия.

Похожая история с котангенсом. Если в некоторую функцию входит , то из её области определения исключаются точки 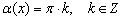. В частности, для функции автоматной очередью расстреливаем следующие значения:

Иными словами: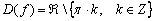

Миниатюра для самостоятельного решения:

Пример 16

Найти область определения функции

Арксинус с арккосинусом, как всегда, выступают хедлайнером математического концерта, и этого стоило дождаться, поскольку кроме нахождения области определения вы сможете научиться решать двойные неравенства (или повторить их).

Если в некоторую функцию входит или , то на её область определения накладывается ограничение в виде двойного неравенства: .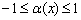

Пример 17

Найти область определения функции

Решение: составим двойное неравенство:

Действия с двойным неравенством очень похожи на действия с «обычным» одинарным неравенством. Конечная цель преобразований – добиться, чтобы в середине остался только «икс».

Сначала избавимся в средней части от константы, для этого вычтем из каждой части неравенства «тройку»:

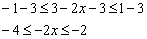
Умножим все три части неравенства на –1. Поскольку множитель отрицателен, то знаки самих неравенств необходимо «развернуть» в противоположную сторону:

Умножим все части неравенства на :

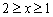
Запишем ответ, переставив знаки неравенств в привычном порядке, а то по-арабски как-то получилось – от «единицы» до «двух» справа налево.

Ответ: область определения: или

Несложный заключительный пример для самостоятельного решения:

Пример 18

Найти область определения функции

Хотелось разобрать более трудные примеры со сложными функциями когда, скажем, под квадратный корень вложена дробь или логарифм, но для этого нужно рассказывать про метод интервалов, который сейчас наверняка запутает значительную часть аудитории. В этой связи я решил перенести объяснения на урок о нулях и интервалах знакопостоянства функции, где постараюсь вернуться к нахождению области определения сложных функций. А на данный момент лучше усвоить меньше, да качественнее!

Желаю успехов!

Решения и ответы:

Пример 2: Область определения:

Пример 4: Решение: найдём нули знаменателя:

Ответ: область определения:

Пример 6: Решение: найдём область определения:

Ответ:

Пример 8: Решение: решим неравенство . Парабола пересекает ось абсцисс в точках . Поскольку , то ветви параболы направлены вниз.
Ответ: область определения:
Примечание: Неравенства вида и (+ такие же строгие неравенства + неравенства с противоположными знаками), где – положительное число, легко решаются аналитически.
Перенесём «единицу» в правую часть: .
Умножим обе части неравенства на –1: .
Из каждой части извлекаем квадратный корень, при этом «икс» необходимо заключить под знак модуля: .
Согласно правилу раскрытия модуля, которое можно найти в школьных формулах:
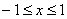, то есть в итоге и получен наш отрезок .

Пример 10: Решение: решим неравенство . Парабола касается оси в точке , причём, ветви параболы направлены вверх. Таким образом, функция 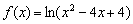не определена в единственной точке.
Ответ: область определения

Пример 12: Решение: составим и решим систему:


Ответ: область определения: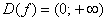

Пример 14: Решение: составим и решим систему:


Ответ: область определения
Примечание: неравенство разрешимо как с помощью анализа расположения параболы относительно оси абсцисс, так и аналитически.
Перенесём «двойку» в правую часть: . Из каждой части извлечём квадратный корень, при этом «икс» необходимо заключить под знак модуля: . Согласно правилу раскрытия модуля (см. Горячие формулы школьного курса математики): , что в точности соответствует объединению интервалов .

Пример 16: Решение: область определения функции задаётся системой:


Ответ:

Пример 18: Решение: составим и решим двойное неравенство:

Ответ: область определения: