
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взаимное расположение прямых в пространстве

| 
|

|
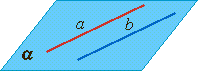
| Пересекающиеся прямые: лежат в одной плоскости, имеют одну общую точку. | Параллельные прямые: лежат в одной плоскости, не имеют общих точек (не пересекаются) | Скрещивающиеся прямые: не лежат в одной плоскости, не имеют общих точек (не пересекаются) |
| Параллельность плоскостей Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют ни одной общей точки. α∥β. | 
|
| Признак параллельности двух плоскостей Теорема. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости , то эти плоскости параллельны. Если а∥а1 и b∥b1, то α∥β. | 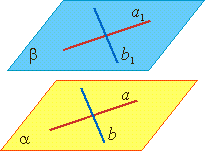
|
Свойства параллельных плоскостей
 Вели α∥β и они пересекаются с γ, то а∥b.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Вели α∥β и они пересекаются с γ, то а∥b.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
|  Если α∥β и AB∥CD, то АВ = CD. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Если α∥β и AB∥CD, то АВ = CD. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
|
"Перпендикулярность прямых и плоскостей.Векторы в пространстве"
| Параллельный перенос Введём на плоскости декартовы координаты xОу. Преобразование некоторой фигуры F, при котором произвольная ее точка А (х;у) переходит в другую точку А (х+a; y+b), где а и b постоянные, называется параллельным переносом; Параллельный перенос есть движение. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. | 
|
Понятие вектора
Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила.
Геометрически векторы изображаются направленными отрезками. Направленный отрезок называется вектором. Вектор характеризуется следующими элементами: 1) начальной точкой (точкой приложения); 2 )направлением; 3) длиной («модулем вектора»).
Если начало вектора — точка А, а его конец — точка В, то вектор обозначается  или или 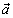 .
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления. Обозначается: .
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления. Обозначается:  .
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора .
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора 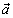 . Обозначается . Обозначается  . .
|
 векторы
векторы 


|
Два вектора называются равными, если они совмещаются параллельным переносом. АВСD — параллелограмм, 
|

|
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если векторы 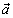 и и  коллинеарны и их лучи сонаправлены, товекторы коллинеарны и их лучи сонаправлены, товекторы 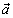 и и  называются сонаправленными. Обозначаются называются сонаправленными. Обозначаются 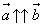 . Если векторы . Если векторы 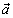 и и 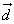 коллинеарны, а их лучи не являются сонаправленными, то векторы коллинеарны, а их лучи не являются сонаправленными, то векторы 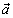 и и 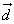 называютсяпротивоположно правленными. Обозначаются называютсяпротивоположно правленными. Обозначаются 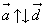 . Нулевой вектор условились считать сонаправленным с любым вектором. . Нулевой вектор условились считать сонаправленным с любым вектором.
|
 коллинеарные векторы:
коллинеарные векторы: 
|
Свойство коллинеарных векторов
Если векторы 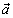 и и  коллинеарны и коллинеарны и  , то существует число k такое, что , то существует число k такое, что 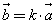 . причем если k > 0, то векторы . причем если k > 0, то векторы 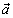 и и  сонаправленные, если k < 0, то противоположно направленные. сонаправленные, если k < 0, то противоположно направленные.
| |
Правило треугольника Каковы бы ни были точки А, В, С, имеет место векторное равенство:

| 
|
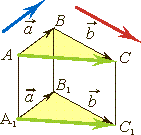
Рисунки иллюстрируют сложение коллинеарных векторов с помощью параллельного переноса.

| Если при сложении векторов 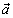 и и  по правилу треугольника точку А заменить другой точкойА1, то вектор по правилу треугольника точку А заменить другой точкойА1, то вектор 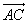 заменится равным ему вектором заменится равным ему вектором 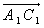 . .
|
Правило параллелограмма
Если векторы 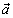 и и  неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм. Диагональ параллелограмма есть сумма двух векторов неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм. Диагональ параллелограмма есть сумма двух векторов 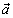 и и  . .
| 
|
Дата добавления: 2015-04-11; просмотров: 233; Мы поможем в написании вашей работы!; Нарушение авторских прав |