
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорияық кiрiспе
9.3.1. Адиабаттық жуықтау. Электрондық термдер.
«Молекула» сөзi «кiшкене масса» деген мағына бередi. Бұл-заттың қасиетi сақталатын, оның ең кiшi бөлшегi. Молекула-күрделi жүйе, ол бiр-бiрiмен белгiлi тәртiппен байланысқан атомдар немесе иондардан құралады.
Атомдардағы сияқты, молекулалардың энергетикалық деңгейлерi, күйлерi және құрылысы жайындағы маңызды мәлiметтер-бұлардың спектрлерiнен алынады. Бiрақта молекулалардың спектрлерi атомдардыкiне қарағанда әлдеқайда көп күрделi, өйткенi олар тек электрондық күйлермен ғана-молекула көлемiнде электрондық зарядтың үлестiрiлуiмен ғана анықталып қоймайды, ядролардың қозғалысымен байланысты басқа да еркiндiк дәрежелерiмен-бұлардың айналысы, тербелiстерiмен және т.т. анықталады.
| |
Нөлiншi жуықтауда ядролар қозғалмайды деп есептеледi, демек электрондардың толқындық функциясы ядролардың координатына, параметрлер ретiнде, тәуелдi болады. Сонымен, қарастырылып отырған жуықтауда ядролар электростатикалық әсерлесудiң центрлерi болып саналады да, ал молекуланың толқындық функциясы тек электрондар координаттарына тәуелдi болады. Молекуладағы электрондар жүйесiнiң En(r) энергиясы ядролардың потенциалдық энергиясы ролiн атқарады.  -ядролардың ара қашықтығы, n-электрондық күйлердi анықтайтын кванттық сандар жиыны. En(r) шамалары молекуланың электрондық термдерi деп аталады. Бұлар атомдардағы сияқты сандар емес, ядролар орындарының (координаты) функциялары болып табылады.
-ядролардың ара қашықтығы, n-электрондық күйлердi анықтайтын кванттық сандар жиыны. En(r) шамалары молекуланың электрондық термдерi деп аталады. Бұлар атомдардағы сияқты сандар емес, ядролар орындарының (координаты) функциялары болып табылады.
Молекулалардың электрондық термдерi жеке атомдардың термдерiне қарағанда әлдеқайда күрделi болады. Атомдағы сияқты емес молекуладағы электрондық бұлттың белгiлi толық импульс моментi болмайды. Мұның себебiн сызықтық молекула мысалында қарастырайық. Осы жағдайда ядролардың ара қашықтығымен анықталатын оқшауланған бағыт болады. Кеңiстiкте айналыс жасайтын молекуладағы ядролар өзiмен бiрге электрондарды iлестiредi, демек электрондардың импульс моментi өзгерiске ұшырайды. Екi атомды молекула өрiсi цилиндрлiк симметриялы болатындықтан, электрондар жүйесiнiң Гамильтон операторы азимуттық бұрышқа тәуелдi болмайды. Бұл электрондық моменттiң оқшауланған бағытқа проекциясы сақталады және квантталады дегендi бiлдiредi, өйткенi оған (проекцияға) молекуланың бүтіндей айналуы әсер етпейдi. Бiр электронды күйлердiң орбиталық моментiнiң сызықтық молекула осiне проекциясы l кванттық санымен (l орбиталық кванттық санына пара-пар) сипатталады. Атомдардағы сияқты, l кванттық санының сан мәндерiне молекулалардың бiр электронды күйлерiнiң әрiптiк символдары (белгiлерi) (s-, p-, d-күйлерiне ұқсастырып) сәйкес қойылады:
l 0 1 2 3 ....
күй s p d j ....
| |
L 0 1 2 3 ...
күй S P D F
L санының максимум мәнi:  . Екi атомды молекулалардың қоздырылған электрондық стационар күйлерi L кванттық санымен ғана емес, толық спиннiң S кванттық санымен де сипатталады. Екi атомның S1 және S2 спиндерi моменттердi қосудың жалпы ережелерi бойынша қосылады:
. Екi атомды молекулалардың қоздырылған электрондық стационар күйлерi L кванттық санымен ғана емес, толық спиннiң S кванттық санымен де сипатталады. Екi атомның S1 және S2 спиндерi моменттердi қосудың жалпы ережелерi бойынша қосылады:
S=S1+S2,...çS1+S2ê, S саны күйдiң мультиплеттiгiн анықтайды. Мультиплеттiлiк ескерiлгенде молекуланың электрондық күйлерiн атомдық күйлердi белгiлеулерге ұқсас белгiлейдi: 2s+1L. Мысалы, 1S, 3S, 1P және т.т. күйлерi.
9.3.2. Екi атомды молекуланың энергетикалық күйлерi. Бұларды электрондық, тербелiс және айналыс құраушыларына бөлу
Молекуланың мүмкін болатын энергетикалық күйлерiн анықтау есебiн жеңiлдету үшін молекулалық толық толқындық функцияны жеткiлiктi дәрежедегi жуықтауда мына көбейтiндi түрінде өрнектеуге болады:
 (9.1)
(9.1)
Бұл Шредингер теңдеуiн жеке электрондық, тербелiс және айналыс толқындық функциясы үшін шешуге мүмкіндiк бередi, яғни Шредингер теңдеуi мына үш теңдеуге жiктеледi:
 (9.2а),
(9.2а),  (9.2б)
(9.2б)
 (9.2в)
(9.2в)
Бұларды шешкенде yе1, yе2, yе3,...; yu1, yu2,...; yr1, yr2,... меншiктi толқындық функциялар және Ее1, Ее2,...; Еu1, Еu2,...; Еr1, Еr2,...меншiктi энергия мәндерi анықталады.
Қарастырылып отырған (9.1) жуықтауда (адиабаттық) молекуланың Е толық энергиясы бiр-бiрiнен тәуелсiз-Ее электрондық,Еu тербелiс және Еr айналыс үш құраушыдан тұрады:
 (9.3.)
(9.3.)
Толық толқындық функцияның (9.1) түрінде болуы мына шарт
 (9.4.)
(9.4.)
| |
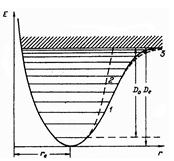
(9.3.) формуладағы әрбiр мүше нақты мәндер қабылдайды. Ее, Еu, Еr берiлгенде молекуланың толық энергиясы белгiлi электрондық-тербелiс-айналыс күйге сәйкес келетiндей мәнге ие болады. Сонда бiр-бiрiнен алшақ орналасқан электрондық деңгейлер, тығызырақ орналасқан тербелiс деңгейлерi, бұдан да жақын орналасқан айналыс деңгейлер жиынтығы алынады (9.1-сурет).

9.1-сурет
Молекула бiр күйден басқа күйге ауысқанда бiр мезгiлде толық энергияның барлық үш бөлiгi (электрондық-тербелiс-айналыс) бiрдей өзгеруi мүмкін. Бұл молекулалардың шығару және жұтылу спектрлерiнде бiлiнедi-спектр құрамында үш құрылым-электрондық, тербелiс және айналыс құрылымдары болады.
Жиiлiктер шартына сәйкес, сәуле шығару және жұтылу ауысулары үшін мына теңдiк орындалады:

мұндағы Е¢¢ және Е¢ -төменгi және жоғары электрондық-тербелiс-айналыс деңгейлерiнiң сәйкес энергиялары, және
 . vu-спектрдiң тербелiс (жолақтық) құрылымын, vr-жолақтың айналыс (нәзiк) құрылымын сипаттайды.
. vu-спектрдiң тербелiс (жолақтық) құрылымын, vr-жолақтың айналыс (нәзiк) құрылымын сипаттайды.
| |
 берiлген жағдайдағы әр түрлі
берiлген жағдайдағы әр түрлі  мәндерiне, ал жолақтардағы нәзiк түзілiстiң жеке сызықтары -берiлген
мәндерiне, ал жолақтардағы нәзiк түзілiстiң жеке сызықтары -берiлген  және
және  жағдайдағы әр түрлі
жағдайдағы әр түрлі  мәндерiне сәйкес келедi.
мәндерiне сәйкес келедi.
Электрондық деңгейлер арасындағы айырма ~ 1-10 эВ. Бұлардың арасындағы ауысулар нәтижесiнде жиiлiктерi ~ 1014-1015Гц электромагниттiк сәуле шығарылады (не жұтылады), яғни мұндай спектрлер спектрдiң көрiнетiн және ультракүлгiн аймақтарында жатады. Егер  =0, яғни электрондық күй тұрақты (өзгермеген жағдайда) болып, тербелiс энергия өзгергенде тербелiс спектрлерi пайда болады. Осы жағдайдағы тербелiс энергиясының өзгерiсiнен айналыс энергиясы да өзгередi. Тербелiс энергиясы үшін
=0, яғни электрондық күй тұрақты (өзгермеген жағдайда) болып, тербелiс энергия өзгергенде тербелiс спектрлерi пайда болады. Осы жағдайдағы тербелiс энергиясының өзгерiсiнен айналыс энергиясы да өзгередi. Тербелiс энергиясы үшін  ~10-1-1эВ, бұған vu~1012-1014 Гц жиiлiк сәйкес келедi. Демек, спектр жақын және алыс инфрақызыл аймақта жатады.
~10-1-1эВ, бұған vu~1012-1014 Гц жиiлiк сәйкес келедi. Демек, спектр жақын және алыс инфрақызыл аймақта жатады.
Егер  =0,
=0,  =0 болып, молекуланың тек
=0 болып, молекуланың тек  айналыс энергиясы өзгеретiн болса, онда таза айналыс спектрлерi пайда болады.
айналыс энергиясы өзгеретiн болса, онда таза айналыс спектрлерi пайда болады.  ~10-3-10-2 эВ, бұған vr~109-1011 Гц жиiлiк сәйкес келедi. Таза айналыс спектрлерi спектрдiң алыс инфрақызыл және субмиллиметрлiк аймағында орналасады.
~10-3-10-2 эВ, бұған vr~109-1011 Гц жиiлiк сәйкес келедi. Таза айналыс спектрлерi спектрдiң алыс инфрақызыл және субмиллиметрлiк аймағында орналасады.
9.3. Екi атомды молекуланың айналыс спектрлерi.Молекулалардың ядролары қатаң бекiтiлген деп ұйғарып айналыс спектрлерiн қарастырайық. Бұл ротатор моделi, молекула құрамына кiретiн массалары m және m атомдар қайсыбiр осьтi айналып қозғала алады. Атомдардың инерция моментi бұлардың центрлерi арқылы өтетiн оське қатысты I=mr2-ге тең, мұндағы  келтiрiлген масса, r-атомдардың (ядролардың) ара қашықтығы.Қатаң ротатор моделi үшін молекуланың энергетикалық күйлерi (9.2 в) формуласымен бейнеленедi, бұған мына айналыс термдерi сәйкес келедi
келтiрiлген масса, r-атомдардың (ядролардың) ара қашықтығы.Қатаң ротатор моделi үшін молекуланың энергетикалық күйлерi (9.2 в) формуласымен бейнеленедi, бұған мына айналыс термдерi сәйкес келедi
 (9.5)
(9.5)
мұндағы  (9.6)
(9.6)
| |
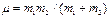 -келтiрiлген масса, re-ядроаралық қашықтық, см; J= 0, 1, 2,... айналыс кванттық саны.
-келтiрiлген масса, re-ядроаралық қашықтық, см; J= 0, 1, 2,... айналыс кванттық саны.

 J
J
 4
4

 3
3


 2
2

 1
1
0





 v 9.2-сурет
v 9.2-сурет





2B
Спектр 2В жиiлiгiнен басталып, 2В интервалымен жоғарырақ жиiлiктер жағына қарай жалғасады (9.2-сурет). Айналыс спектрiне тән жиiлiктер w»109-1011с-1; бұларға сәйкес толқын ұзындық ~0,01см (спектрдiң алыс инфрақызыл және микротолқындық аймақтары).
9.3.4.Екi атомды молекуланың тербелiс-айналыс спектрi.
Молекулалардың айналыс қозғалысын қарастырғанда атомдар (және бұлардың ядролары) қатаң бекiтiлген деп ұйғарылды. Алайда ядролар тепе-теңдiк қалып маңайында тербелiс жасай алады. Осы тербелiстердiң энергиясы мына формуламен анықталады:
 (9.8)
(9.8)
Екi атомды молекуланың потенциалдық қисығы Морзе функциясымен (1929) сапалық дұрыс бейнеленедi
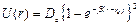 (9.9)
(9.9)
b шамасы молекулалық тұрақтылармен анықталады. Осы потенциалмен Шредингер теңдеуiн шығару тербелiс энергиясы үшін тербелiстердiң ангармонизмi ескерiлген формуланы бередi
 (9.10)
(9.10)
мұндағы wехе-ангармонизм коэффициентi,υ=0,1,2,...
Таза тербелiс спектрi болмайды, өйткенi молекулалар негiзгi және қозған тербелiс күйлерiнде айналыс күйлерiнiң қатары бойынша үлестiрiлген болады.
| |
 ,
, 
ал айналыс термдерi  .
. 
Сондықтан жалпы түрде тербелiс-айналыс термi былай жазылады:
 (9.11)
(9.11)
9.3-суретте u¢ және u¢¢ екi тербелiс күйлерi үшін айналыс деңгейлерiнiң жүйесi келтiрiлген. u және J мәндерi әр
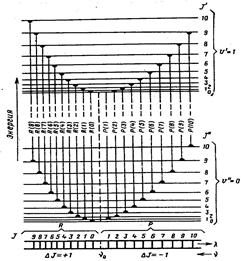
9.3-сурет
түрлі деңгейлер арасындағы кванттық ауысулар тербелiс-айналыс спектрiн бередi; u және J үшін сұрыптау ережелерi
 (9.12а)
(9.12а) 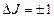 (9.12б)
(9.12б)
Оңайлық үшін, алдымен айналыс (нәзiк) түзілiстi елемей, тек тербелiс ауысулар қарастырылады. Сонда айналыс энергетикалық деңгейлер қосылып кетедi де, спектрде тербелiс ауысуларына сәйкес келетiн тек кеңейген жолақтар байқалады.
| |
 -ға ешқандай шектеу болмайды, бiрақ u өскенде де,
-ға ешқандай шектеу болмайды, бiрақ u өскенде де,  өскенде де жолақтардың жалпы интенсивтiлiгi төмендейдi; бұл қосымша сұрыптау ережесi болып табылады. Бөлмелiк температура жағдайында спектрлерде әдетте бар болғаны 2-3 осындай ауысу байқалады. 2-0, 3-0 және т.т. обертондар деп аталады. Негiзгi тон (негiзгi жолақ) 1-0 ауысуына сәйкес келедi (тербелiс ауысулар белгiлеуiнде алдымен u¢, одан кейiн u¢¢ көрсетiледi).
өскенде де жолақтардың жалпы интенсивтiлiгi төмендейдi; бұл қосымша сұрыптау ережесi болып табылады. Бөлмелiк температура жағдайында спектрлерде әдетте бар болғаны 2-3 осындай ауысу байқалады. 2-0, 3-0 және т.т. обертондар деп аталады. Негiзгi тон (негiзгi жолақ) 1-0 ауысуына сәйкес келедi (тербелiс ауысулар белгiлеуiнде алдымен u¢, одан кейiн u¢¢ көрсетiледi).
Айналыс термдерi ескерiлмеген жағдайда обертондардың тербелiс жиiлiктерi (толқындық сандары  ), термдер айырмасынан оңай табылады, яғни
), термдер айырмасынан оңай табылады, яғни

 (9.13)
(9.13)
Тек қозған күйлердiң қатысуымен пайда болатын жолақтар (мысалы, 2-1, 3-2 жолақтары) «ыстық» жолақтар деп аталады, өйткенi u=1, 2,... күйлердiң жеткiлiктi қоныстануы тек затты қыздырғанда алуға болады.
Обертондар жиiлiктерi және негiзгi жиiлiк мәндерiнен ve тербелiс жиiлiктерiн және vexe ангармониялықты есептеп табуға болады. Ол үшін алдымен 1-обертон мен негiзгi жиiлiк арасындағы бiрiншi айырмалар, 2-обертон мен 1-обертон арасындағы және т.т. бiрiншi айырмалар есептелiнедi.
Жалпы түрде бiрiншi айырмалар мынаған тең
 (9.14)
(9.14)
бұл өзiнiң физикалық мағынасы бойынша тербелiс күйлерiнiң көршi термдерiнiң ара қашықтығына тең.
Егер 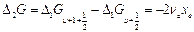 (9.15)
(9.15)
болса онда vexe ангармоникалық тұрақтыны есептеуге, демек оны бiлу арқылы (9.14) формула бойынша ve тербелiс жиiлiгiн анықтауға болады. Барлық тербелiс кванттық сандары бойынша (umax дейiн) бiрiншi айырмалардың қосындысы молекуланың D0 диссоциация энергиясына тең.
| |
Екі атомды молекуланың мүмкін болатын барлық энергетикалық күйлер жүйесін жалпы түрде мына теңдеумен өрнектеуге болады:
 (9.16)
(9.16)
Жолақ спектрлердiң күрделi көрiнiсiн жақсы ұғыну үшін, алдымен (9.16) теңдеудегi айналыс термдерiн ескермейтiн боламыз, өйткенi бұлардың энергиясы Те және G(u) термдерiне қарағанда көп кiшi. Электрондық спектрлердiң тек тербелiс түзілiсiне тоқталамыз. Бұл электрондық спектрлердiң дөрекi тербелiстiк түзілiсi прогрессиялар осы жағдайда тербелiс жолақтарының орны мына теңдеумен бейнеленедi:
 (9.17)
(9.17)
мұндағы  -таза электрондық ауысу,
-таза электрондық ауысу,  тербелiс жиiлiгi мен
тербелiс жиiлiгi мен 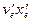 ангармониялық тұрақты тиiсiнше
ангармониялық тұрақты тиiсiнше  және
және  -ден үлкен де, кiшi де болуы мүмкін.
-ден үлкен де, кiшi де болуы мүмкін.
u мәндерi әр түрлі болатын ауысуларға ешқандай шектеу жоқ-бiр электрондық күйдiң әрбiр тербелiс деңгейi басқа электрондық күйдің кез-келген тербеліс деңгейімен комбинация жасай алады. u¢¢ мәнi тұрақты болатын жолақтар сериялары u¢ бойынша прогрессиялар, ал u¢ тұрақты жолақтар сериялары u¢¢ бойынша прогрессиялар деп аталады (9.4-сурет).
Du=u¢-u¢¢ мәнi тұрақты жолақтар сериялары диагоналдық сериялар (секвенциялар) деп аталады.

| |
Бiрақта спектрде осындай кванттық ауысулардың шектеулi саны байқалады. Бұл Франк-Кондон принципiмен байланысты; ол былайша тұжырымдалады: молекула бiр электрондық күйден басқасына ауысқанда электрондық тығыздықтың қайта үлестiрiлуiнiң тез өтетiндiгi соншалықты, ауыр ядролардың ара қашықтықтары өзгерiп үлгермейтiн болады.
Бiр электрондық ауысуға жататын спектрде байқалатын барлық жолақтарды Деландр кестесi (9.1-кесте) түрінде өрнектеуге болады. Бұл кестеде әрбiр клеткаға электрондық-тербелiс ауысуына сәйкес толқындық сан мәнi жазылады. Деландр кестесiн құру электрондық ауысудың тербелiс түзілiсiн құрайтын (байқалатын) жолақтар канттарының қайсысы қандай u¢-u¢¢ ауысуға жататын анықтауға саяды. Электрондық спектрлердiң тербелiс құрылымын талдау (теңдестiру) 0-0 ауысуын табудан басталады. Өйткенi бұған қатысты u¢ және u¢¢ бойынша прогрессияларды табу оңай болады. Әрбiр прогрессияның (Деландр кестесiнiң бойлық және тiк жолы) өзiнiң аз өзгеретiн тербелiс интервалы болады, ол негiзiнен  және
және  -дан тәуелдi бiрiншi
-дан тәуелдi бiрiншi  және
және  айырмалар шамасымен анықталады.
айырмалар шамасымен анықталады.
9.1-кесте
Деландр кестесi
  u¢¢
u¢ u¢¢
u¢
| ... | ||||
| v00 | v01 | v02 | v03 | ||
| v10 | v11 | v12 | v13 | ||
| v20 | v21 | v22 | v23 | ||
| v30 | v30 | v32 | v33 | ||
| ... |
Деландр кестесi (9.1, 9.2-кестелер) бойынша қозған және негiзгi электрондық күйлер үшін ve және vexe мәндерiн оңай есептеп табуға болады. ve және vexe мәндерiн анықтау үшін алдымен көлденең және тiк қатардағы көршi клеткалардағы сандардың бiрiншi айырымын табады. Осы айырымдар (9.14) өрнегiнен белгiлi шамаға сәйкес келедi:
 (9.14а)
(9.14а)
Егер ендi екiншi айырымды есептесе, онда олар екi еселенген ангармониялық тұрақтыға сәйкес келедi:
 , (9.15а)
, (9.15а)
| |
Көлденең және тiк қатарлардағы екiншi айырмаларды орташалап  және
және 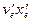 мәндерiн табуға, бұдан кейiн табылған шамаларды бiрiншi айырым теңдеуiне қойып, орташаланған
мәндерiн табуға, бұдан кейiн табылған шамаларды бiрiншi айырым теңдеуiне қойып, орташаланған  және
және  мәндерiн анықтауға болады.
мәндерiн анықтауға болады.
Молекулалардың айналыс күйлерiнiң өзгерiсiмен байланысқан жолақтардың нәзiк, айналыс түзілiсiн қарастыру үшін, мына тұрақты шаманы белгiлеу керек
 (9.18)
(9.18)
Сонда электрондық-тербелiс-айналыс жолағының айналыс (нәзiк) түзілiсi мына теңдеумен өрнектеледi
 (9.19)
(9.19)
бұл тербелiс-айналыс спектрi үшін формулаға ұқсас.
9.2-кесте
Деландр кестесi бойынша молекулалық тұрақтыларды есептеу
 u¢¢
u¢ u¢¢
u¢
| 1-i айы рым дар | 1-i айыр ымдар | ... | орташа | |||||
| v00 | 
| v01 | 
| v02 | ... | ||||
| 1-айыр ымдар | 
| 
| 
| ... | 
| ||||
| v10 | 
| v11 | 
| v12 | ... | 
| |||
| 1-айыр ымдар | 
| 
| 
| ... | 
| ||||
| v20 | 
| v21 | 
| v22 | ... |  
| |||
| ... | ... | ... | ... | ... | ... | ... | ... | ||
| орташа | 
| 
| 
|

| ... |
Электрондық ауысулар болған жағдайда ядролардың тепе-теңдiк ара қашықтығы өзгеретiн болса, онда айналыс тұрақтысы өзгередi. Электрондық-тербелiс-айналыс спектрiндегi айналыс ауысулары үшін сұрыптау ережесi
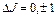 (9.20)
(9.20)
Осыған байланысты, (9.19) формуладан жалпы жағдайда, спектрде (жолақтың нәзiк түзілiсiнде) P-, Q-, R- үш тармақ байқалуы мүмкін:  -ге сәйкес келедi.
-ге сәйкес келедi.
Әр тармақ сызықтарының өз теңдеуi болады:
P-тармақ:  (9.21)
(9.21)
Q-тармақ:  (9.22)
(9.22)
R-тармақ:  (9.23)
(9.23)
Жиiлiктердiң J кванттық санынан осы (9.21-23) параболалық тәуелдiлiктерi Фортра диаграммалары көмегiмен кескiнделедi. (9.21-23) теңдеулерi тербелiс-айналыс спектрлерi теңдеулерiне ұқсас қорытылады. Электрондық-тербелiс-айналыс спектрiндегi Р- және R-тармақтары үшін теңдеулер тербелiс-айналыс спектрiндегi Р- және R-тармақтары теңдеулерiне ұқсас. Бұлардың арасындағы айырмашылық vu¢u¢¢ құрамында тек vu емес vе де бар, ал (В¢u-В¢¢u) айырымы оң да, терiс те мәндер қабылдай алады, өйткенi қоздырылған электрондық күйде ядроаралық қашықтық негiзгi күйдегiден үлкен де, кiшi де болуы мүмкін.
9.3.6. Молекулалық жолақ канты. Деландр формуласы. Фортра диаграммасы.
Кейбiр жағдайларда есептеуге ыңғайлы болуы үшін R- және Р-екi тармақты бiр формуламен өрнектейдi:
 (9.24)
(9.24)
мұндағы R-тармақ үшін (m=J+1) m=1, 2,...
Р- тармақ үшін (m=J) m=-1, -2,...
Егер (В¢u-В¢¢u)<0 болса, онда J немесе çm ê өскенде (9.23) теңдеуiндегi квадраттық мүше (3В¢u-В¢¢u)J сызықтық мүшенi «басып озады», R-тармақтағы сызықтардың толқындық сандары бiртiндеп өсуiн тоқтатады, бұдан кейiн керi жаққа «бұрылады» және кеми бастайды.
| |
9.5-суретте CN-молекуласының бiр жолағы үшін айналыс (нәзiк) түзілiсi сызықтары орындарының J кванттық санына (çm êсанына) тәуелдiлiгiн көрсететiн Фортра диаграммасы келтiрiлген.
Ендi жолақ канты деген не-соған тоқталайық.
Молекулалық спектрлердi әр түрлі газдағы электр разрядтары шығаратын жарығынан бақылауға болады. Дисперсиясы үлкен емес құрал арқылы бақыланатын олар бiр жағынан айқын шекарамен-кантпен шектелген, ал екiншi жағынан бiртiндеп нөлге дейiн әлсiрейтiн жолақтар түрінде болады.

9.5-сурет
Осы интенсивтiктiң бiртiндеп төмендеуi жолақтың ерекшеленуi (оттенение) деп аталады. Оның ұзын немесе қысқа толқындар жағынан орналасуына байланысты қызыл немесе күлгiн ерекшелену болып бөлiнедi.
Кейде жолақтардың бiрнеше канты болады, кейбiр жағдайларда кант тiптi болмауы да мүмкін. Ажыратқыштық күшi жоғары құралдармен жолақтардың көпшiлiгi жеке сызықтарға ажыратылады, бұлардың ара қашықтықтары канттан алыстаған сайын бiртiндеп өседi. Жолақтардың бiр мезгiлде пайда болуы, спектрдiң белгiлi бөлiгiнде орналасуы, ерекшеленудiң бiрдей болуы, кант санының бiрдей болуы сияқты бiрқатар ортақ қасиеттерге ие болуына қарай олар жолақтар жүйесiне бiрiгедi.
| |
 (9.24а)
(9.24а)
мұндағы c, d, e-берiлген жолақ үшін тұрақтылар. Сызықтың нөмiрiн белгiлейтiн m бүтін санына оң да, терiс те мәндер берiледi. m=0 сызық спектрде болмайды. Кванттық механика бойынша нөлiншi сызық айналыс болмайтын екi күй арасындағы тиым салынған ауысуға сәйкес келедi.
l=388,3 нм канты бар жолақ үшін ең бiр қарапайым молекулалардың бiрi-CN циан радикалы жағдайында (9.24а) формула мына түрде жазылады
v=25797685+3,848m+0,0675m2 [cм-1] (9.24б)
9.5-суретте (9.24б) формула бойынша есептелiп тұрғызылған график (Фортра параболасы) келтiрiлген.
m=0, ±1, ±2,... болғандағы көлденең сызықтардың параболамен қиылысу нұктелерi спектр (жолақ) сызықтарының толқындық сандарын бередi. Суреттен жолақ канты және ерекшеленуi қалай пайда болатындығын көруге болады. Кант-парабола төбесiне сәйкес келетiн шеткi сызық, ерекшелену төбеден алыстаған сайын сызықтардың бiртiндеп аралары алшақтап, сирей тұсуi. Параболаның жеке бөлiктерi тармақтар деп аталады. 9.5-суретте кескiнделген Фортра параболасында R-тармақ (m мәндерiнiң оң таңбалы болатын жағдай) және Р- тармақ (m-нiң терiс мәндерi жағдайында) бар. Параболаның төбесi аймағында сызықтар ұйысып, спектрограммада әдетте ажыратылмайды. Сызықтардың ұйысу аймағын кейде жолақтың басы, ал сиректеу аймағы-жолақ құйрығы деп аталады.
9.3.7. Екi атомды молекулалардың диссоциация энергиясы
Диссоциация энергиясы-молекуланың, әсiресе, әр түрлі химиялық процестер реакцияларының жылу мөлшерiн анықтаған жағдайда өте маңызды сипаттамасы. Екi атомды молекулалардың диссоциация энергиясын сызықтық интерполяцияның мына жуық формуласы бойынша анықтауға болады:
 (9.25)
(9.25)
Бұл өрнектi  тербелiс интервалдарының u-дан сызықтық тәуелдi болатындығынан және u өзiнiң umax мәнiне жақындағанда бұлардың нөлге ұмтылатындығынан алуға болады. Сондықтан мына өрнектi
тербелiс интервалдарының u-дан сызықтық тәуелдi болатындығынан және u өзiнiң umax мәнiне жақындағанда бұлардың нөлге ұмтылатындығынан алуға болады. Сондықтан мына өрнектi
| |
 , нөлге тең деп қабылдауға болады, осыдан
, нөлге тең деп қабылдауға болады, осыдан
 (9.26)
(9.26)
өйткенi vexe<<ve. umax мәнiн термдер энергиясы үшін (9.10) өрнекке қойып, молекуланың атомдарға ыдырау (диссоциация) энергиясын анықтауға болады:

Ескеретiн нәрсе, (9.25) жеткiлiктi жуық формула, ~20% дәлдiкпен нәтиже алуға болады.
Осы (9.25) формуланы және
 (9.27)
(9.27)
өрнегiн пайдаланып зерттеп отырған молекуланың D0 диссоциация энергиясын бағалауға болады.
Те электрондық терм мәнiн мына формула арқылы алуға болады:
 (9.28)
(9.28)
9.5. Жұмыстың орындалу ретi
1. Көмiр электродтарынан электр доғасы шығаратын жарықтың спектрiн суретке түсіру:
ДФС-8 спектрографының саңылау енi-0,01мм, толқын ұзындық шкаласының бөлiктерi-«360», «380», «415»; көмiр электродтардың ұзындығы-4-5см, электродтар аралығы ~2мм.
2. CN молекуласы спектрiне талдау жүргізуге қажеттi салыстыру спектрi-Fe спектрiн суретке түсіру.
3. Спектрлердi суретке түсіру жағдайлары 9.3-кестеде келтiрiлген
9.3-кесте
| спектр | l,нм | кассета орны | Гартман диафраг масы | Доға тоғы А | Экспозиция уақыты, с |
| Fe | |||||
| CN(көмiр) | |||||
| Fe | |||||
| CN(көмiр) | |||||
| Fe | |||||
| CN(көмiр) |
| |
9.5.1. CN молекуласының шығару спектрiн зерттеу
ДСП-1немесе ПС-18 спектропроекторында ДФС-8 спектрографы үшін Fe спектрi атласын пайдаланып, молекулалық жолақтар канттарының толқын ұзындықтарын анықтау. Жолақтарды нөмiрлеу. Жолақтар канттарының өлшенген (анықталған) толқын ұзындықтарын CN молекуласының энергетикалық диаграммасымен салыстырып (9.6-сурет), CN молекуласы электрондық спектрiнiң тербелiстiк құрылымына теңдестiру жүргізу (әрбiр жолақтың қандай кванттық ауысуда пайда болатындығын анықтау).
Канттардың өлшенген ұзындықтарын толқындық сандарға (см-1) айналдыру.
Алынған нәтижелердi 9.4-кестеге толтыру.
9.4-кесте
| Жолақ ғ | Жолақ кантының толқын ұзындығы l, нм | Кванттық ауысу u®u¢¢ | Жолақ кантының толқындық саны vu¢u¢¢, см-1 |
9.5.2. CN молекуласының меншiктi тербелiс жиiлiгiн, ангармоникалық коэффициентiн және диссоциация энергиясын анықтау
1. Канттардың алынған vu¢u¢¢ толқындық сандарын (9.4-кесте) Деландр кестесiнiң (9.1, 9.2-кестелер) клеткалары бойынша толтырылады.
9.4-кестедегi молекулалық тербелiс жолақтары канттарының vu¢u¢¢ толқындық сандары бойынша (v0-0, v1-0, v1-1, v2-1, v2-2, v3-2) бiрiншi D1v айырманы анықтау, яғни CN молекуласының жоғарғы және төменгi электрондық күйлерiнiң көршi тербелiс термдерiнiң ара қашықтығын анықтау. (9.14), (9.14а) формулаларын және 9.6-суреттi қараңыз.
2. D1v0-1, D1v1-2,... бiрiншi айырма бойынша D2v екiншi айырмасын анықтау
D2v= D1v0-1 - D1v1-2,...
Ескерту: алынған D1v және D2v мәндерi 9.2-Деландр кестесiндегi көршi жолақтар арасындағы 1-және 2-айырмалары
 және
және  мәндерiне сәйкес келедi. Алынған нәтижелердi 9.1-9.2-Деландр кестелерiне толтыру.
мәндерiне сәйкес келедi. Алынған нәтижелердi 9.1-9.2-Деландр кестелерiне толтыру.
3.
| |
 ангармониялық коэффициент мәндерiн анықтау (Деландр кестесi бойынша).
ангармониялық коэффициент мәндерiн анықтау (Деландр кестесi бойынша).
4. (9.14) формуланы пайдаланып молекуланың меншiктi тербелiс жиiлiгiн анықтау.
5. (9.25) және (9.27) формулаларды пайдаланып CN молекуласының D0 диссоциация энергиясын бағалау.
6. (9.28) формула арқылы CN молекуласының Те электрондық терм мәнiн анықтау. Алынған нәтижелердi 9.5-кестеге толтырып, [3; 9] әдебиеттегi деректермен салыстыру.
9.5-кесте
| жолақ канты ның толқын дық саны vu¢u¢¢ | D1v см-1 | D2v см-1 | vехе см-1 | vе см-1 | De Дж | D0 Дж | Te см-1 |

9.7-сурет
| |
9.5.3. CN молекуласының ядроаралық қашықтығын анықтау
1. CN молекуласы спектрi нәзiк түзілiсi көршi екi сызығының орташа қашықтығын (см-1) анықтау. Бұл үшін спектрограмманы МИР-12 микроскопы үстелiне қойып, молекулалық жолақтың нәзiк түзілiсi екi сызығының Dl ара қашықтығы өлшенедi. ДФС-8 спектрографы дисперсиясының мәнi бойынша (0,6нм/мм) Dl (мм) ара қашықтық Dv (см-1) толқындық сандар айырымына айналдырылады. Dv айырма (n-1)-ге бөлiнедi, мұндағы n-өлшенген екi сызық арасына келетiн сызық саны (екi сызықты қоса санағанда).
2. Әр түрлі тербелiс жолақтары үшін табылған көршi екi сызықтың ара қашықтығы мәндерi бойынша (9.6) формуланы пайдаланып молекуланың айналыс тұрақтысы анықталады.
3. I=mr2 өрнегiн пайдаланып, CN молекуласының инерция моментiн анықтау.
4. CN молекуласының r ядроаралық қашықтығын анықтау. Алынған нәтиженi әдебиеттердегi деректермен салыстыру.
Алынған нәтижелердi 9.6-кестеге толтыру.
9.6-кесте
| жолақ u¢®u¢¢ | екi сызық тың ара қашық тығы Dl, мм | n-1 | Dl нм | Dv см-1 | В см-1 | I г×см2 | r см |
Дата добавления: 2014-10-31; просмотров: 701; Мы поможем в написании вашей работы!; Нарушение авторских прав |