Этапы проверки статистических гипотез

1. Формулировка основной гипотезы H₀ и конкурирующей гипотезы H₁. Гипотезы должны быть чётко формализованы в математических терминах.

2. Задание вероятности α, называемой уровнем значимости и отвечающей ошибкам первого рода, на котором в дальнейшем и будет сделан вывод о правдивости гипотезы.

3. Расчёт статистики φ критерия такой, что:

§ её величина зависит от исходной выборки ;

§ по её значению можно делать выводы об истинности гипотезы H₀;

§ сама статистика φ должна подчиняться какому-то известному закону распределения, т.к. сама φ является случайной в силу случайности .

4. Построение критической области. Из области значений φ выделяется подмножество 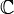таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство . Это множество 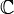и называется критической областью.

5. Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику φ и по попаданию (или непопаданию) в критическую область 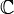выносится решение об отвержении (или принятии) выдвинутой гипотезы H₀.

22. Последовательные схемы испытаний.

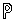Определение :Будем говорить, что имеется схема независимых, однородных повторных испытаний или полиномиальная схема, если = , i=1,2,...,n, т.е. n раз повторяется один и тот же эксперимент. Число m=| | называется числом исходов в отдельном испытании, а число n - числом испытаний. Независимость испытаний означает, что вероятности ( ) не зависят от исходов предыдущих испытаний, но могут зависеть от номера k испытания. В случае, когда такой зависимости нет, испытания называются однородными, т.е. если вероятности 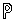( )=p k=1,2,...,n, не зависят от k, в противном случае испытания называются неоднородными.

Определение : Частный случай полиномиальной схемы с двумя исходами в каждом испытании (m=2) называют схемой испытаний Бернулли или просто схемой Бернулли. В этом случае в каждом из экспериментов наблюдают за появлением или непоявлением события A. Вероятность появления события A в любом из экспериментов обозначается p (0 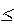p 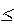1), тогда q=1-p - вероятность непоявления события A. Вероятность появления события A в n испытаниях ровно k раз обозначим P (k). Совокупность вероятностей P (k) называется распределением Бернулли или биномиальным распределением.