
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Естественный” способ
Этот способ применяется тогда, когда известна траектория движения материальной точки. Положение точки  определяется дуговой координатой
определяется дуговой координатой 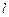 – расстоянием вдоль траектории от выбранного начала отсчета
– расстоянием вдоль траектории от выбранного начала отсчета  (см. рис. 1.).
(см. рис. 1.).
Если известна зависимость дуговой координаты от времени, величина скорости точки определяется по формуле:
 .
.
 Полное ускорение
Полное ускорение 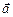 является суммой двух ускорений – тангенциального (или касательного)
является суммой двух ускорений – тангенциального (или касательного)  и нормального (или центростремительного)
и нормального (или центростремительного) 
 .
.
Эти ускорения перпендикулярны друг другу, поэтому модуль полного ускорения равен:
 .
.
Тангенциальное и нормальное ускорения рассчитываются по формулам:
 ,
,  ,
,
где  – радиус кривизны траектории в данной точке.
– радиус кривизны траектории в данной точке.
При любом способе описания движения материальной точки возникает и обратная задача: найти зависимость скорости и положения точки в пространстве от времени, если известна зависимость ускорения от времени. Решить эту задачу можно, зная начальные условия, а именно скорость материальной точки и ее положение в пространстве в тот момент времени, который принимается за начало отсчета.
Вопросы для самоконтроля
1. Скорость материальной точки меняется со временем по закону  Известно, что в начальный момент времени
Известно, что в начальный момент времени  и
и 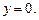 Укажите ошибочныеутверждения:
Укажите ошибочныеутверждения:
а) 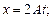 б)
б)  в)
в) 
г)  д)
д)  е)
е) 
ж)  з)
з)  и)
и) 
где 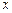 и
и 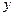 – координаты,
– координаты,  и
и  – проекции скорости на координатные оси,
– проекции скорости на координатные оси,  – величина скорости,
– величина скорости,  – величина ускорения материальной точки.
– величина ускорения материальной точки.
2. Известна зависимость скорости материальной точки  от времени
от времени  Для нахождения радиус-вектора
Для нахождения радиус-вектора  определяющего положение точки в пространстве, необходимо знать:
определяющего положение точки в пространстве, необходимо знать:
а) начальную скорость;
б) начальное положение, т.е. радиус-вектор  в момент времени
в момент времени 
в) начальную скорость и начальное положение;
г) только зависимость 
Укажите правильные утверждения.
3. При движении вдоль криволинейной траектории полное ускорение материальной точки равно:
а)  б)
б)  в)
в) 
г)  д)
д)  е)
е) 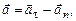
где  и
и  – нормальное тангенциальное ускорения точки.
– нормальное тангенциальное ускорения точки.
Укажите правильные утверждения.
4. Материальная точка движется равномерно по окружности радиуса  . Укажите ошибочные утверждения:
. Укажите ошибочные утверждения:
а)  б)
б)  в)
в)  г)
г) 
где  – скорость точки.
– скорость точки.
5. Материальная точка движется по окружности радиуса  . Скорость точки меняется со временем по закону
. Скорость точки меняется со временем по закону  где
где 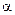 – положительная постоянная. Полное ускорение точки равно:
– положительная постоянная. Полное ускорение точки равно:
а) 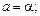 б)
б) 
в) 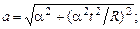 г)
г) 
Укажите правильные утверждения.
Дата добавления: 2015-04-15; просмотров: 263; Мы поможем в написании вашей работы!; Нарушение авторских прав |