
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Пример 1. Радиус-вектор частицы меняется со временем по закону , где –постоянный вектор,
Пример 1. Радиус-вектор частицы меняется со временем 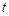 по закону
по закону 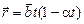 , где
, где  –постоянный вектор,
–постоянный вектор, 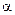 – положительная постоянная. Найти:
– положительная постоянная. Найти:
а) скорость и ускорение частицы в зависимости от времени;
б) промежуток времени 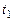 , по истечении которого частица вернется в исходную точку, путь
, по истечении которого частица вернется в исходную точку, путь  , который она пройдет при этом, среднюю
, который она пройдет при этом, среднюю  и среднюю путевую
и среднюю путевую  скорости за время движения.
скорости за время движения.
Р е ш е н и е. Найдем скорость и ускорение частицы: 
 , (2)
, (2)
 .
.
Из условия задачи следует, что в начальный момент времени  радиус-вектор
радиус-вектор 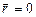 . Это означает, что для нахождения времени
. Это означает, что для нахождения времени 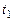 , по истечении которого частица вернется в исходную точку, радиус-вектор
, по истечении которого частица вернется в исходную точку, радиус-вектор 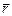 в этот момент времени надо приравнять нулю
в этот момент времени надо приравнять нулю
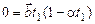 .
.
Откуда следует, что
 .
.
Для нахождения пути  , пройденного частицей, воспользуемся формулой (1). Напомним, что под знаком интеграла стоит модуль скорости частицы. Из выражения (2) следует, что вектор скорости частицы совпадает по направлению с вектором
, пройденного частицей, воспользуемся формулой (1). Напомним, что под знаком интеграла стоит модуль скорости частицы. Из выражения (2) следует, что вектор скорости частицы совпадает по направлению с вектором  до того момента времени
до того момента времени 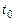 , когда скорость частицы станет равна нулю. Это время, как следует из (1), равно
, когда скорость частицы станет равна нулю. Это время, как следует из (1), равно
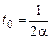 .
.
После этого, вектор скорости изменит свое направление на противоположное, т.е.

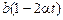 при
при 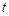 <
< 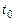
и

 при
при 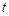 >
> 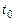 .
.
Таким образом, путь, пройденный телом, будет равен:
 .
.
После подстановки 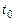 и
и 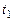 , получаем
, получаем
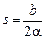 .
.
Надо отметить, что в данной задаче путь, пройденный частицей, можно вычислить иначе. Действительно, поскольку частица, двигаясь по прямой (вдоль вектора  ) вернулась в исходную точку, путь будет равен
) вернулась в исходную точку, путь будет равен
 ,
,
где  – длина радиус-вектора в момент времени
– длина радиус-вектора в момент времени 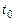 , т.е.
, т.е.
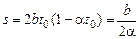 .
.
Вектор перемещения  частицы за все время движения равен нулю (по условию задачи она вернулась в исходную точку), поэтому средняя скорость равна нулю. Средняя путевая скорость за все время движения
частицы за все время движения равен нулю (по условию задачи она вернулась в исходную точку), поэтому средняя скорость равна нулю. Средняя путевая скорость за все время движения 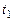 равна
равна
 .
.
Пример 2. Точка движется в плоскости 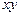 по закону
по закону  ,
,  , где
, где 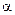 и
и  – положительные постоянные. Найти:
– положительные постоянные. Найти:
а) уравнение траектории материальной точки  ;
;
б) величины скорости  и ускорения
и ускорения  точки в зависимости от
точки в зависимости от 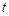 ;
;
в) момент времени 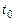 , когда угол между скоростью и ускорением равен
, когда угол между скоростью и ускорением равен  .
.
Р е ш е н и е. а) Для нахождения уравнения траектории исключим из уравнений, приведенных в условии задачи время 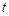 :
:
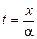 ,
,
 .
.
б) Определим проекции скорости на оси ОХ и  :
:
 ,
,
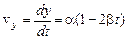 ,
,
и рассчитаем модуль скорости
 .
.
Аналогичным образом рассчитаем величину ускорения:
 ,
,
 ,
,
 .
.
в) Для нахождения времени 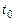 воспользуемся скалярными представлениями произведения вектора скорости и вектора ускорения:
воспользуемся скалярными представлениями произведения вектора скорости и вектора ускорения:
 .
.
С другой стороны
 .
.
Таким образом:
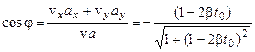 .
.
После подстановки значения угла 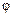 и преобразования этого выражения получаем
и преобразования этого выражения получаем
 .
.
Пример 3. Частица движется по дуге окружности радиуса 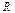 по закону
по закону  , где
, где 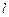 – смещение из начального положения, отсчитываемого вдоль дуги, А и
– смещение из начального положения, отсчитываемого вдоль дуги, А и  – постоянные. Найти полное ускорение частицы в точках: а)
– постоянные. Найти полное ускорение частицы в точках: а) 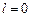 ; б)
; б)  .
.
Р е ш е н и е. Определим зависимость величины скорости от времени:
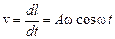 .
.
По определению тангенциальное и нормальное ускорения соответственно равны:
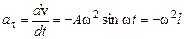 ,
,
 .
.
Таким образом, при 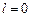 полное ускорение равно:
полное ускорение равно:
 ,
,
а при  :
:
 .
.
Пример 4. Точка движется, замедляясь, по прямой с ускорением, модуль которого зависит от ее скорости  по закону
по закону  , где
, где 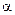 – положительная постоянная. В начальный момент скорость точки равна
– положительная постоянная. В начальный момент скорость точки равна  . Какой путь
. Какой путь  , она пройдет до остановки? За какое время
, она пройдет до остановки? За какое время 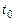 этот путь будет пройден?
этот путь будет пройден?
Р е ш е н и е. Пусть точка движется в положительном направлении оси 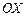 . За начало отсчета координаты
. За начало отсчета координаты 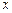 примем точку старта. Поскольку движение замедленное, т.е.
примем точку старта. Поскольку движение замедленное, т.е.  <0, модуль ускорения равен
<0, модуль ускорения равен
 .
.
По условию задачи
 . (3)
. (3)
Для того чтобы решить дифференциальное уравнение (3), надо разделить переменные
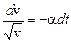 ,
,
а затем проинтегрировать правую (в пределах от начальной скорости  – нижний предел интегрирования, до скорости точки
– нижний предел интегрирования, до скорости точки  в произвольный момент времени
в произвольный момент времени 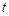 – верхний предел интегрирования) и левую (в пределах от нуля до
– верхний предел интегрирования) и левую (в пределах от нуля до 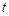 ) части этого уравнения. Таким образом,
) части этого уравнения. Таким образом,
 .
.
Решая это уравнение, находим зависимость скорости точки от времени
 .
.
Так как в момент остановки 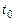 скорость тела равна нулю, получаем
скорость тела равна нулю, получаем
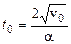 .
.
Путь  пройденный телом, можно найти, воспользовавшись уравнением
пройденный телом, можно найти, воспользовавшись уравнением
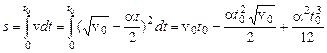 .
.
После подстановки в это уравнение 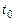 , получаем
, получаем
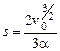 .
.
Этот способ нахождения пути не единственный. Вернемся к уравнению (3). Умножим и разделим левую часть этого уравнения на 
 ,
,
т.к.  , получаем
, получаем
 .
.
При интегрировании этого уравнения учтем, что в момент остановки 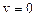 и
и 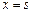 , тогда, решая уравнение
, тогда, решая уравнение
 ,
,
получим:
 .
.
Видно, что второй способ нахождения пути проще, чем первый.
Пример 5. Точка движется, замедляясь, по окружности радиуса  так, что в каждый момент времени ее тангенциальное и нормальное ускорения по модулю равны друг другу. В начальный момент
так, что в каждый момент времени ее тангенциальное и нормальное ускорения по модулю равны друг другу. В начальный момент  скорость точки равна
скорость точки равна  . Найти зависимости:
. Найти зависимости:
а) скорости точки от времени и от пройденного пути  ;
;
б) полного ускорения от скорости и пройденного пути.
Р е ш е н и е. а)По условию задачи  . Учитывая, что движение замедленное, запишем
. Учитывая, что движение замедленное, запишем
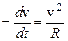 . (4)
. (4)
Разделив переменные,

и решая полученное дифференциальное уравнение
 ,
,
найдем зависимость скорости от времени
 .
.
Для нахождения зависимости скорости от пройденного пути, умножим и разделим левую часть уравнения (4) на приращение дуговой координаты 
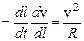 ,
,
т.к. 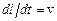 , получим дифференциальное уравнение
, получим дифференциальное уравнение
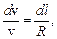
решая которое,
 ,
,
найдем зависимость скорости от пройденного пути
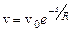 . (5)
. (5)
б) Полное ускорение точки равно  . Учитывая, что по условию задачи
. Учитывая, что по условию задачи  , найдем зависимость полного ускорения от скорости
, найдем зависимость полного ускорения от скорости
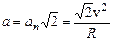 .
.
Подставляя в это выражение (5), определим зависимость полного ускорения от пройденного пути
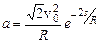 .
.
 Пример 6.Частица
Пример 6.Частица  движется в одну сторону по траектории, представленной на рис. 2 с тангенциальным ускорением
движется в одну сторону по траектории, представленной на рис. 2 с тангенциальным ускорением 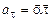 , где
, где 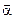 – постоянный вектор, совпадающий по направлению с осью ОХ, а
– постоянный вектор, совпадающий по направлению с осью ОХ, а 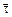 – единичный вектор, связанный с частицей
– единичный вектор, связанный с частицей  и направленный по касательной к траектории в сторону возрастания дуговой координаты
и направленный по касательной к траектории в сторону возрастания дуговой координаты 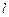 . Найти скорость частицы в зависимости от
. Найти скорость частицы в зависимости от 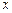 , если в точке
, если в точке 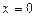 ее скорость равна нулю.
ее скорость равна нулю.
Р е ш е н и е. По определению
 ,
,
то есть
 ,
,
где 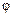 – угол между вектором
– угол между вектором 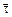 и вектором
и вектором 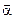 ( см. рис. 3). Вектор
( см. рис. 3). Вектор 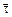 – единичный вектор, поэтому
– единичный вектор, поэтому  . Умножим и разделим левую часть этого уравнения на приращение дуговой координаты
. Умножим и разделим левую часть этого уравнения на приращение дуговой координаты 

 ,
,
откуда получаем
 .
.
Но 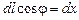 , тогда
, тогда
 .
.
Интегрируя это уравнение,
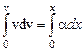 ,
,
найдем зависимость скорости частицы от координаты 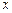
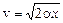 .
.
Пример 7. Точка движется по плоскости так, что ее тангенциальное ускорение  , а нормальное ускорение
, а нормальное ускорение 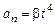 , где
, где 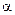 и
и  – положительные постоянные,
– положительные постоянные, 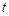 – время. В момент
– время. В момент  точка покоилась. Найти зависимости от дуговой координаты
точка покоилась. Найти зависимости от дуговой координаты 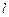 радиуса кривизны
радиуса кривизны  траектории точки и ее полного ускорения
траектории точки и ее полного ускорения 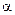 .
.
Р е ш е н и е. Найдем зависимости скорости и дуговой координаты точки от времени, учитывая, что в начальный момент точка покоилась. Будем считать, что в точке старта значение дуговой координаты равно нулю. Учитывая, что
 , и
, и  ,
,
получим

и
 . (6)
. (6)
По условию задачи
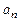
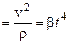 ,
,
откуда
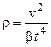 .
.
Подставляя в это уравнение  и значение
и значение  , найденное из (6), определим зависимость радиуса кривизны траектории от дуговой координаты
, найденное из (6), определим зависимость радиуса кривизны траектории от дуговой координаты
 .
.
Найдем полное ускорение
 .
. 
Подставляя  , получим зависимость полного ускорения от дуговой координаты
, получим зависимость полного ускорения от дуговой координаты
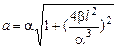 .
.
Дата добавления: 2015-04-15; просмотров: 1108; Мы поможем в написании вашей работы!; Нарушение авторских прав |