
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи для самостоятельного решения. Задача 1.За промежуток времени точка прошла половину окружности радиуса Вычислить за это время: а) средне-путевую скорость ; б) модуль
Задача 1.За промежуток времени  точка прошла половину окружности радиуса
точка прошла половину окружности радиуса 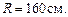 Вычислить за это время: а) средне-путевую скорость
Вычислить за это время: а) средне-путевую скорость  ; б) модуль средней скорости
; б) модуль средней скорости 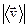 ; в) модуль среднего вектора полного ускорения
; в) модуль среднего вектора полного ускорения  , если точка двигалась с постоянным тангенциальным ускорением.
, если точка двигалась с постоянным тангенциальным ускорением.
О т в е т. а)  б)
б)  в)
в) 
Задача 2.Радиус- вектор точки  относительно начала координат меняется по закону
относительно начала координат меняется по закону  , где
, где 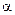 и
и  – постоянные,
– постоянные,  и
и  – орты осей
– орты осей 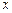 и
и 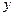 . Найти: а) уравнение траектории точки
. Найти: а) уравнение траектории точки  ; б) зависимости от времени скорости
; б) зависимости от времени скорости  , ускорения
, ускорения 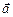 и модули этих величин; в) зависимость от времени угла
и модули этих величин; в) зависимость от времени угла 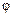 между векторами
между векторами  и
и 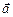 .
.
О т в е т. а)  ; б)
; б)  ,
,  ,
,  ,
,  ; в)
; в)  .
.
Задача 3.В момент времени  частица вышла из начала координат в положительном направлении оси
частица вышла из начала координат в положительном направлении оси 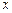 . Ее скорость меняется по закону
. Ее скорость меняется по закону  , где
, где  – начальная скорость, модуль которой
– начальная скорость, модуль которой  ,
,  с. Найти: а) координату
с. Найти: а) координату 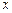 частицы в момент времени 6, 10 и 20 с; б) моменты времени, когда частица будет находиться на расстоянии 10см от начала координат.
частицы в момент времени 6, 10 и 20 с; б) моменты времени, когда частица будет находиться на расстоянии 10см от начала координат.
О т в е т. а)  ; 0.24, 0 и –2 м; б) 1.1, 9 и 11с.
; 0.24, 0 и –2 м; б) 1.1, 9 и 11с.
Задача 4.Частица движется в положительном направлении оси 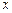 так, что ее скорость меняется по закону
так, что ее скорость меняется по закону  , где
, где 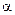 – положительная постоянная. Имея в виду, что в момент
– положительная постоянная. Имея в виду, что в момент  она находилась в точке
она находилась в точке  , найти: а) зависимости от времени скорости и ускорения частицы; б) среднюю скорость частицы за время, в течении которого она пройдет первые
, найти: а) зависимости от времени скорости и ускорения частицы; б) среднюю скорость частицы за время, в течении которого она пройдет первые  метров пути.
метров пути.
О т в е т. а)  ,
,  ; б)
; б)  .
.
Задача 5.Точка движется в плоскости 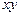 по закону
по закону 
 где
где  и
и  – положительные постоянные. Найти: а) путь
– положительные постоянные. Найти: а) путь  проходимый точкой за время
проходимый точкой за время  б) угол между скоростью и ускорением точки.
б) угол между скоростью и ускорением точки.
О т в е т. а)  б)
б) 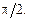
Задача 6.Точка движется в плоскости 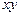 с постоянным ускорением
с постоянным ускорением  направление которого противоположно положительному направлению оси
направление которого противоположно положительному направлению оси  Уравнение траектории частицы имеет вид
Уравнение траектории частицы имеет вид  где
где 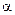 и
и  – положительные постоянные. Найти скорость частицы
– положительные постоянные. Найти скорость частицы  в начале координат.
в начале координат.
О т в е т. 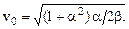
Задача 7.Воздушный шар начинает подниматься с поверхности земли. Скорость его подъема постоянна и равна  Благодаря ветру шар приобретает горизонтальную компоненту скорости
Благодаря ветру шар приобретает горизонтальную компоненту скорости  где
где 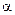 – постоянная,
– постоянная, 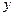 – высота подъема. Найти зависимости от высоты подъема: а) величины сноса шара
– высота подъема. Найти зависимости от высоты подъема: а) величины сноса шара  б) полного, тангенциального и нормального ускорений шара.
б) полного, тангенциального и нормального ускорений шара.
О т в е т. а)  б)
б) 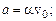


Задача 8.Частица движется в плоскости 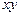 со скоростью
со скоростью  где
где  и
и  – орты осей
– орты осей 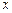 и
и 
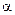 и
и  – постоянные. В начальный момент частица находилась в точке
– постоянные. В начальный момент частица находилась в точке  Найти: а) уравнение траектории
Найти: а) уравнение траектории  б) радиус кривизны траектории в зависимости от
б) радиус кривизны траектории в зависимости от 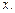
О т в е т. а)  б)
б) 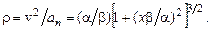
Задача 9.Точка движется по окружности со скоростью  , где
, где 
 . Найти ее полное ускорение в момент, когда она пройдет
. Найти ее полное ускорение в момент, когда она пройдет  длины окружности после начала движения.
длины окружности после начала движения.
О т в е т.  .
.
Задача 10.Точка движется по дуге окружности радиуса  . Ее скорость зависит от пройденного пути
. Ее скорость зависит от пройденного пути  по закону
по закону  , где
, где 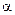 – постоянная. Найти угол
– постоянная. Найти угол 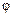 между вектором полного ускорения и вектором скорости в зависимости от
между вектором полного ускорения и вектором скорости в зависимости от  .
.
О т в е т.  .
.
Дата добавления: 2015-04-15; просмотров: 280; Мы поможем в написании вашей работы!; Нарушение авторских прав |