Системы отсчета. Инерциальные системы отсчета.

Для описания движения тела или используемой модели – материальной точки может быть применен векторный способ описания, когда положение интересующего нас объекта задают с помощью радиус-вектора отрезка, направленного от тела отсчета в интересующую нас точку, положение которой в пространстве может изменяться со временем. Геометрическое место концов радиус-вектора называют траекторией движущейся точки.

2.1. Системы координат.

Другим способом описания движения тела является координатный, в котором с телом отсчета жестко связывают определенную систему координат.

В механике, и в физике вообще, в разных задачах удобно пользоваться различными системами координат. Наиболее употребимыми являются, так называемые, декартова, цилиндрическая и сферическая системы координат.

1) Декартова система координат: вводятся три взаимно перпендикулярных оси с заданными масштабами по всем трем осям (линейки). Начало отсчета по всем осям берется от тела отсчета. Пределы изменения каждой из координат от до .

Радиус-вектор, задающий положение точки, определяется через её координаты как

. (2.1)

Малый объем в декартовой системе:

,

или в бесконечно малых приращениях:

(2.2)

2) Цилиндрическая система координат: в качестве переменных выбираются расстояние от оси , угол поворота от оси x и высота вдоль оси от тела отсчета.

Радиус-вектор определяется:

(2.3)

Пределы изменения координат:

Декартовы координаты выражаются через цилиндрические

следующим образом:

, . (2.4)

Элемент объема:

(2.5)

3) Сферическая система координат: вводится расстояние от тела отсчета до интересующей точки и углы

поворота и , отсчитываемые от осей и , соответственно.

Радиус-вектор – функция переменных

,

пределы изменения координат:

Декартовы координаты связаны со сферическими следующими соотношениями

(2.6)

Элемент объема в сферических координатах:

(2.7)

2.2. Система отсчета.

Для построения системы отсчета систему координат необходимо дополнить часами. Часы могут находиться в различных точках пространства, поэтому их нужно синхронизовать. Синхронизация часов производится с помощью сигналов. Пусть время распространения сигнала из точки, где произошло событие, до точки наблюдения равно . Тогда наши часы должны показывать время , если часы в точке события в момент его появления показывают время . Такие часы будем считать синхронизированными.

Если расстояние от точки пространства, где произошло событие, до точки наблюдения , то .

В классической механике принимается, что скорость распространения сигнала . Поэтому вводятся одни часы во всем пространстве.

Совокупность тела отсчета, системы координат и часов образуют Систему отсчета (СО).

Имеется бесконечное множество систем отсчета. Опыт дает, что пока скорости невелики по сравнению со скоростью света , то линейные масштабы и промежутки времени не изменяются при переходе от одной системы отсчета к другой.

Иначе говоря, пространство и время абсолютны в классической механике.

Если , то масштабы и интервалы времени зависят от выбора СО, т.е. пространство и время становятся понятиями относительными. Это уже область релятивистской механики.

2.3. Инерциальные системы отсчета (ИСО).

Итак, мы стоим перед выбором системы отсчета, в которой могли решать задачи механики (описывать движение тел и устанавливать причины, его вызывающие). Выясняется, что далеко не все системы отсчета равноправны не только при формальном описании задачи, но, что гораздо важнее, по-разному представляют причины, вызывающие изменение состояние тела.

Систему отсчета, в которой законы механики формулируются наиболее просто, позволяет установить первый закон Ньютона, который постулирует существование инерциальных систем отсчета – ИСО.

I закон классической механики – закон инерции Галилея-Ньютона.

Существует такая система отсчета, в которой материальная точка, если исключить её взаимодействие со всеми остальными телами, будет двигаться по инерции, т.е. сохранять состояние покоя или равномерного прямолинейного движения.

Это – инерциальная система отсчета (ИСО).

В ИСО изменение движения материальной точки (ускорение) обусловлено только её взаимодействием с другими телами, но не зависит от свойств самой системы отсчета.

ИСО – бесконечное множество, но по физическим свойствам все они эквивалентны, т.е. абсолютной, выделенной среди множества инерциальных систем, ИСО нет.

2.4. Реализация ИСО.

Инерциальные системы отсчета играют исключительно важную роль, поскольку позволяют в наиболее простой и удобной форме записать законы механики. Именно в таких системах отсчета и выполняются сформулированные Ньютоном законы. Однако сразу же возникает резонный вопрос – реализуются ли такие системы в природе, другими словами, насколько велика практическая польза от введения ИСО?

Безусловно, инерциальная система отсчета – идеализация, как и абсолютно свободное тело.Поэтому практический выбор ИСО зависит от заданной точности описания того или иного явления или задачи.

А. Естественно, интересующую нас систему отсчета удобно связать с поверхностью Земли. Однако оказывается, что выбранная система отсчета неинерциальная. Неинерциальность такой системы отсчета обусловлена вращением Земли вокруг собственной оси (суточным вращением). Т.е. тело, находящееся на поверхности Земли, даже не взаимодействую с другими телами, будет приобретать ускорение. Сделаем численную оценку эффекта, вычислив центростремительное ускорение точки, расположенной на экваторе:

,

( ).

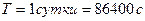Что дает нам полученный результат? Много это или мало? Как известно, все познается в сравнении.

Степень неинерциальности выбранной системы отсчета определяется путем сопоставления с ускорением свободного падения у поверхности Земли.

Полученное значение составляет около 0,3 % от ускорения свободного падения .

Поэтому для обычных механических задач, не связанных с прецизионными физическими измерениями, отсчет можно производить относительно поверхности Земли.

Рассмотрим теперь систему отсчета, связанную с Солнцем – гелиоцентрическую. Неинерциальность этой системы отсчета связана с движением Земли по орбите вокруг Солнца (годовое вращение). Соответствующее ускорение определяется через угловую скорость, равную

,

и составляет

, или от .

(Радиус орбиты Земли ).

Если выбрать в качестве инерциальной системы отсчета галактическую, то для оценки её неинерциальности необходимо учесть, что Солнце вращается вместе с планетами солнечной системы вокруг центра нашей Галактики со скоростью порядка , а расстояние до центра нашей Галактики составляет примерно ( = ). Тогда соответствующее ускорение равно

, или от ,

т.е. система отсчета, связанная с неподвижными звездами, может считаться инерциальной с очень хорошей степенью точности.