Основное уравнение динамики. Основные задачи динамики.

6.1. Основное уравнение динамики.

Основное уравнение динамики есть математическое выражение второго закона Ньютона:

. (6.1)

Записанное через импульс, оно имеет вид:

. (6.2)

Мы записали второй закон Ньютона как опытный закон. Однако его можно представить как следствие закона сохранения импульса. В самом деле, если система изолирована (замкнута), то имеем

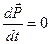. (6.3)

Если система не изолирована (или рассматриваем отдельные тела внутри замкнутой системы), то

. (6.4)

Функцию координат и скорости материальной точки, определяющую производную ее импульса по времени называют силой. Поэтому основное уравнение динамики или 2-ой закон Ньютона записывается

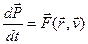или . (6.5)

Это уравнение - векторное, поэтому оно может быть представлено в виде системы из трех (по числу измерений пространства) скалярных уравнений. Однако, в силу принципа независимости движения по взаимно перпендикулярным направлениям (осям), может сохраняться часть проекций импульса 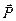, например, на одну из осей, тогда для других проекций записываются уравнения типа (6.3). Конкретное содержание эти уравнения получают лишь тогда, когда определена функция . Установление таких зависимостей - основная задача динамики.

Пример: сохранение импульса по оси x: 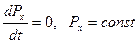, т.е. и 1-ый закон Ньютона формально становится как бы следствием 2-го закона Ньютона.

Однако выделение 1-го закона Ньютона в “самостоятельный” физический закон принципиально необходимо, поскольку он указывает такую систему отсчета (ИСО), в которой справедлива запись 2-го закона Ньютона.

Рассмотрим два тела, образующих замкнутую систему. В такой системе выполняется закон сохранения импульса:

,

отсюда

, или .

Т.о., получаем 3-ий закон Ньютона

В силу того, что в замкнутой системе , получаем важное следствие.

Сумма сил, действующих внутри замкнутой системы тел (внутренних сил) равна нулю: .

6.2. Основные задачи динамики.

Два основных типа задач динамики:

1) Известна зависимость координаты от времени , при этом находим .

2) Известна сила , находим .

6.3. Уравнение движения тела с переменной массой.

Во многих задачах, представляющих практический интерес, масса тела изменяется в процессе движения.

Получим уравнение для движения тела с переменной массой, пользуясь инвариантностью законов в различных ИСО. В качестве примера рассмотрим движение ракеты:

а) пусть в момент времени ракета имеет массу ;

б) присоединяемая (отделяемая) масса 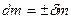имеет скорость 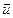относительно массы m;

в) введем инерциальную 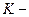систему отсчета, скорость которой совпадает со скоростью ракеты в момент времени , т.е. в указанный момент времени ракета покоится в 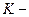системе.

г) за время от до 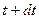материальная точка приобретает в 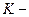системе импульс за счет внешних сил , действующих со стороны окружающих тел или силового поля, и за счет присоединяемой (отделяемой) массы :

Уравнение Мещерского:

. (6.6)

Получили уравнение Мещерского – основное уравнение динамики материальной точки с переменной массой. Оно описывает движение тела, к которому присоединяется масса со скоростью (Внимание: знак + в уравнении (6.6) – присоединение массы). Будучи полученным в ИСО, в силу принципа относительности Галилея это уравнение справедливо в любой ИСО.

Рассмотрим частные случаи уравнения Мещерского.

А) Реактивная сила: . Если 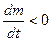- потеря массы и скорость выброса массы 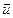направлена в противоположную сторону скорости , то реактивная сила есть сила, вызывающая ускорение ракеты (вектор направлен против вектора ).

Б) Если скорость , то и уравнение Мещерского совпадает по форме с основным уравнением динамики, но только с массой, зависящей от времени, :

Пример такого движения: движение цистерны, из которой выливается вода.

В) Случай когда (т.е. присоединяемая масса неподвижна в выбранной системе отсчета или отделяемая масса становится неподвижной в этой системе отсчета), то

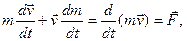
т.е. получили основное уравнение динамики для тела с переменной массой.

Пример движения: движущаяся платформа, на которую сыпется песок из неподвижного бункера.

Формула Циолковского (Сивухин, I, стр. 114-122)