
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принцип относительности и преобразования Галилея. 3.1. Принцип относительности Галилея.
3.1. Принцип относительности Галилея.
Все инерциальные системы отсчета (ИСО) по своим механическим свойствам эквивалентны; т.е. принцип относительности Галилея устанавливает равноправие всех инерциальных систем отсчета.
Это равноправие проявляется в том, что все законы механики одинаковы (инвариантны) во всех ИСО. Отсюда следует, что никакими механическими опытами, проводимыми внутри какой-либо ИСО, нельзя установить покоится ли эта система отсчета или движется равномерно и прямолинейно.
Придадим принципу относительности Галилея математическую форму
Рассмотрим две ИСО:  и
и 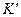 . В каждой свои тела отсчета
. В каждой свои тела отсчета  и
и  , свои часы. Любое событие с точки зрения наблюдателя из
, свои часы. Любое событие с точки зрения наблюдателя из 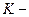 системы характеризуется координатами и временем: (
системы характеризуется координатами и временем: (  ). С точки зрения наблюдателя из системы
). С точки зрения наблюдателя из системы 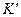 : (
: (  ).
).

|
Найдем преобразование координат события при переходе от системы 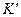 к
к 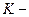 системе. Выберем оси декартовых систем координат
системе. Выберем оси декартовых систем координат  системы параллельно соответствующим осям
системы параллельно соответствующим осям 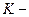 системы, причем так, чтобы оси
системы, причем так, чтобы оси  и
и  совпали между собой. Пусть
совпали между собой. Пусть  система движется относительно системы
система движется относительно системы  со скоростью
со скоростью 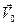 , направленной вдоль оси
, направленной вдоль оси  . Возьмем за начало отсчета времени момент, когда начала координат
. Возьмем за начало отсчета времени момент, когда начала координат  и
и  совпали. Тогда
совпали. Тогда
 (3.1)
(3.1)
Для радиус-векторов формула преобразования координат при переходе от системы  к
к  системе имеет вид:
системе имеет вид:
 (3.2)
(3.2)
Т.о., получаем
 преобразования Галилея. (3.3)
преобразования Галилея. (3.3)
Преобразование скорости:
дифференцируем по времени  в системе
в системе 
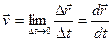 (3.4)
(3.4)
и дифференцируем по времени  в системе
в системе 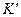
 . (3.5)
. (3.5)
Итак, получаем:
 (3.6)
(3.6)
Примечание: Если принять абсолютность пространства, т.е. постулировать, что длины отрезков не зависят от состояния движения (или покоя), то из прямого и обратного преобразования радиус-векторов

и равноправия ИСО, т.е.  , следующего из принципа относительности Галилея, получаем условие абсолютной одновременности:
, следующего из принципа относительности Галилея, получаем условие абсолютной одновременности:  . Время инвариантно во всех ИСО.
. Время инвариантно во всех ИСО.
Ускорение: 
 и
и 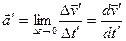 (3.7)
(3.7)
Получаем инвариантность ускорения:
 (3.8)
(3.8)
3.2. Инварианты и инвариантность законов Ньютона.
Помимо ускорения в классической механике существуют и другие инварианты:
1) расстояние между двумя точками;
2) относительная скорость двух тел;
3) Для описания взаимодействия тел вводится величина  , характеризующая интенсивность этого взаимодействия и называемая силой. В механике силой называют меру механического действия на данное тело других тел. Это действие вызывает изменение скорости тела или его частей, также его деформацию.
, характеризующая интенсивность этого взаимодействия и называемая силой. В механике силой называют меру механического действия на данное тело других тел. Это действие вызывает изменение скорости тела или его частей, также его деформацию.
Сила может действовать на тело как при непосредственном контакте с другими телами, так и посредством создаваемых телами полей (например, поле тяготения, электромагнитное поле).
Сила  векторная величина и в каждый момент времени она характеризуется численным значением, направлением в пространстве и точкой приложения. Сложение сил производится по правилу параллелограмма сил. Прямая, вдоль которой направлена сила, называется линией действия силы.
векторная величина и в каждый момент времени она характеризуется численным значением, направлением в пространстве и точкой приложения. Сложение сил производится по правилу параллелограмма сил. Прямая, вдоль которой направлена сила, называется линией действия силы.
Сила инвариантна относительно преобразований Галилея: 
В гауссовой системе единиц сила измеряется в динах:  .
.
В системе СИ единицей измерения силы служит 1 Ньютон.  .
.
Сила всегда есть функция разности координат (парная сила, например) и относительных скоростей
(например, сила сопротивления)  .
.
Пример.
Сила упругости в 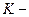 системе:
системе:  , а в
, а в 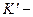 системе:
системе:  .
.
Воспользуемся преобразованием координат 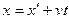 :
:

4) масса – инвариант классической механики: 
Отсюда получаем, что законы механики инвариантны относительно преобразований Галилея:
II закон Ньютона инвариантен в любой ИСО.
Дата добавления: 2015-04-15; просмотров: 322; Мы поможем в написании вашей работы!; Нарушение авторских прав |