Импульс. Закон сохранения импульса. 4.1. Импульс (количество движения).

4.1. Импульс (количество движения).

Импульс частицы – векторная величина, вводимая как

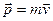- (4.1)

одна из основных мер механического движения частицы – количество движения.

Импульс системы материальных точек:

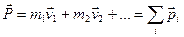(4.2)

Импульс играет в механике (и, как мы увидим далее, не только в классической) исключительно важную роль, поскольку для него может выполняться закон сохранения.

4.2. Закон сохранения импульса.

Введем понятие «замкнутая система» - совокупность материальных точек (или тел), взаимодействующих друг с другом, но не взаимодействующих с другими (внешними) телами. Понятие замкнутой (иначе изолированной) системы справедливо только в ИСО, поскольку в неинерциальных системах, как мы увидим позже, возникают дополнительные силы.

Закон сохранения полного импульса замкнутой системы во времени – экспериментальный факт:

(4.3)

Импульсы отдельных частиц, образующих замкнутую систему могут изменяться со временем, но полный импульс такой системы сохраняется во времени.

Или иначе в проекциях:

(4.4)

Этот закон - следствие однородности пространства, т.е. если замкнутую систему перенести из одного места пространства в другое, поставив при этом все тела в ней в те же условия, в каких они находились в прежнем положении, то это не отразится на ходе последующих явлений.

4.3. Столкновение двух частиц.

Пусть замкнутая система состоит из двух материальных точек, которые сталкиваются друг с другом. В любой момент времени импульс системы сохраняется:

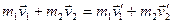(4.5)

Это уравнение верно для упругих и неупругих ударов. Введем изменение скоростей материальных точек за промежуток времени :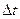

,

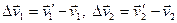тогда

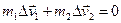, или по модулю ,

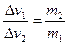т.е. получили, что изменение скоростей обратно пропорционально массам. Поделив на время, за которое произошло изменение скорости, получим

. (4.6)

Т.о., под действием одинаковых по величине сил тело получит тем меньшее ускорение, чем больше его масса. Сообщить одно и то же ускорение большому телу значительно труднее, чем маленькому, т.е. труднее изменить состояние тела. Отсюда вытекает известное определение массы как меры инертности тела.

4.4 Сохранение массы в процессах столкновения.

В классической (нерелятивистской) механике из принципа относительности Галилея и закона сохранения импульса вытекает сохранение полной массы системы взаимодействующих частиц.

Рассмотрим абсолютно неупругое столкновение двух частиц в ИСО (интересно именно неупругое, поскольку, скорее всего, именно оно должно приводить к изменениям массы).

В 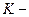системе интересующий нас процесс описывается уравнением:

(5.8)

В системе 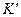, которая движется со скоростью относительно системы :

(5.9)

Запишем преобразования скорости при переходе от 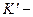системы к системе :

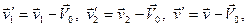(5.10)

Подставив (5.10) в (5.9) и учитывая (5.8), получаем

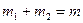, (5.11)

что дает аддитивность массы и ее сохранение.

В то же время, из релятивистской механики известно соотношение 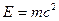, которое устанавливает связь между массой и энергией, выделяющейся в процессе взаимодействия тел (частиц). Поэтому аддитивность и закон сохранения массы верны лишь приближенно, в меру справедливости преобразования Галилея.

Рассмотрим примеры процессов, протекающих с выделением энергии, и определим, с какой точностью выполняется закон сохранения массы.

Химические реакции. Ломоносов, в подтверждение закона сохранения массы, провозгласил - сумма масс до реакции равна сумме масс после реакции. Но мы знаем, что в химических реакциях выделяется энергия, следовательно, это сохранение массы приближенное.

Пример реакции:

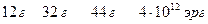
При таких количествах вещества изменение массы в результате реакции составляет

Итак, относительное изменение массы равно

.

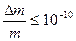т.е. с очень большой точностью масса сохраняется. Поэтому к таким взаимодействиям применим нерелятивистский закон сохранения массы.

Ядерные реакции. В ядерной физике реакции протекают с очень большим энерговыделением, поэтому (дефект массы) становится заметной величиной, т.е. сравнимой с массами участвующих в реакции частиц. Очевидно, что в таких взаимодействиях классический закон сохранения массы уже не работает.