Вращение вокруг неподвижной оси

Кинематика твердого тела

Абсолютно твердым телом или просто твердым телом в механике называют идеализированную систему материальных точек, все расстояния между которыми при движении системы не изменяются с течением времени. Различают пять видов движения твердого тела: 1) поступательное, 2) вращательное вокруг неподвижной оси, 3) плоское, 4) движение вокруг неподвижной точки, 5) свободное. Первые два вида движения являются основными. Остальные виды движения твердого тела можно свести к их совокупности.

В данном пособии рассматриваются первые три вида движения.

Поступательное движение

Поступательным движением твердого тела называют такое движение, при котором любая прямая, связанная с телом, все время остается параллельной своему начальному положению. При таком движении все точки твердого тела совершают за один и тот же промежуток времени равные перемещения. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Это позволяет свести изучение поступательного движения тела к изучению движения отдельной точки (см. раздел “Кинематика материальной точки”).

Вращение вокруг неподвижной оси

Это такое движение твердого тела, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

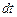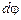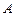Пусть твердое тело, вращаясь вокруг неподвижной оси , совершило за время бесконечно малый поворот на угол . Найдем модуль перемещения точки твердого тела. Положение точки 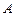относительно некоторой точки , расположенной на оси вращения (см. рис. 1.) зададим радиус-вектором , тогда

,

где 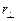– радиус окружности, вдоль которой движется точка 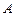.Разделив правую и левую части этого уравнения на 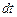, получим

, (1)

где

(2)

мгновенная угловая скорость вращения твердого тела. Из этого определения следует, что угловая скорость – скалярная величина, имеющая размерность радиан в секунду.

Однако угловую скорость можно определить как векторную величину. При изучении сложных движений твердого тела представление угловой скорости в виде вектора дает возможность получить большую

наглядность, а также резко упростить как анализ движения, так и соответствующие расчеты. Векторные величины, введенные искусственно, называются аксиальными векторами или псевдовекторами. Используя уравнение (1), из которого следует, что

,

введем аксиальный вектор , определяемый векторным произведением

.

Тогда уравнение (2) запишем в векторном виде

,

откуда следует, что бесконечно малый угол поворота , также является аксиальным вектором. На рис.1. показано правление векторов и .

Если аксиальный вектор продифференцировать по времени, то в результате получится новый аксиальный вектор

называемый угловым ускорением.

Уравнение (1) также можно записать в векторном виде

. (3)

Это уравнение дает нам связь между линейной 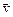и угловой скоростями.

Продифференцировав (3) по времени, найдем полное ускорение точки А:

,

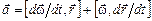или

,

где – мгновенное угловое ускорение твердого тела.

Так как ось вращения неподвижна, угловое ускорение 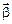коллинеарно угловой скорости , поэтому вектор направлен по касательной к траектории движения и является тангенциальным ускорением точки А, величина этого ускорения равна

.

Вектор направлен к центру окружности, вдоль которой движется точка А, и является ее нормальным ускорением, величина которого равна

.