
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Плоское движение твердого тела. Плоским движением твердого тела называют такое движение, при котором все точки тела движутся в плоскостях
Плоским движением твердого тела называют такое движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости. Примером такого движения может служить качение цилиндра по плоскости. Для изучения такого движения достаточно рассмотреть движение точек тела, лежащих в какой-либо одной плоскости. Это означает, что тело можно считать плоским.
Выберем две произвольные точки твердого тела 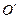 и
и 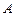 Положение тела в некоторой неподвижной системе отсчета
Положение тела в некоторой неподвижной системе отсчета 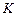 можно определить, задав, например, радиус-вектор
можно определить, задав, например, радиус-вектор  точки
точки 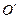 и угол
и угол 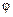 между радиус-вектором
между радиус-вектором 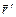 , проведенным из точки
, проведенным из точки 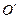 в точку
в точку 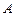 , и некоторым фиксированным направлением в
, и некоторым фиксированным направлением в 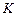 - системе отсчета (рис. 2).
- системе отсчета (рис. 2).
 Введем вспомогательную
Введем вспомогательную 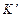 - систему отсчета, жестко связанную с точкой
- систему отсчета, жестко связанную с точкой 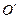 . Пусть за время
. Пусть за время 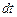 точка
точка 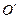 совершила перемещение
совершила перемещение 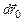 , а вектор
, а вектор 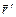 повернулся на угол
повернулся на угол  . Тогда перемещение
. Тогда перемещение  точки
точки 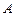 в
в 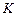 - системе можно записать в виде
- системе можно записать в виде
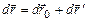 ,
,
где 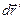 – перемещение точки
– перемещение точки 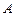 в
в 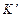 системе. Поскольку расстояние между точками
системе. Поскольку расстояние между точками 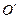 и
и 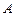 в процессе движения остается неизменным, перемещение
в процессе движения остается неизменным, перемещение 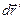 обусловлено вращением тела вокруг неподвижной в
обусловлено вращением тела вокруг неподвижной в 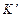 - системе оси, проходящей через точку
- системе оси, проходящей через точку 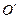 и равно
и равно  . Подставляя это выражение в предыдущее и разделив обе части на
. Подставляя это выражение в предыдущее и разделив обе части на 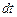 , получим
, получим
 , (4)
, (4)
где  – угловая скорость вращения тела в
– угловая скорость вращения тела в 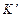 - системе. Таким образом, плоское движение твердого тела можно представить как совокупность двух движений – поступательного (движение
- системе. Таким образом, плоское движение твердого тела можно представить как совокупность двух движений – поступательного (движение 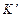 - системы, связанной с точкой
- системы, связанной с точкой 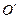 , относительно системы
, относительно системы 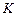 ) и вращательного (вокруг оси, проходящей через точку
) и вращательного (вокруг оси, проходящей через точку 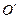 ). Заметим, что, если вектор
). Заметим, что, если вектор 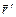 при вращении повернулся на некоторый угол
при вращении повернулся на некоторый угол 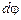 , то и любая прямая, жестко связанная с телом, повернется на такой же угол. Другими словами, величина поворота тела на угол
, то и любая прямая, жестко связанная с телом, повернется на такой же угол. Другими словами, величина поворота тела на угол 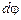 , а значит и угловая скорость
, а значит и угловая скорость 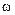 не зависит от выбора точки
не зависит от выбора точки 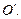
Докажем, что плоское движение можно свести к чисто вращательному движению. Так как точки 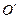 и
и 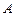 – две произвольные точки твердого тела, длина вектора
– две произвольные точки твердого тела, длина вектора 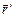 в процессе движения остается неизменной, а поэтому
в процессе движения остается неизменной, а поэтому
 .
.
Дифференцируя это соотношение по времени, получим
 ,
,
или
 ,
,
где 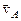 и
и  – скорости точек
– скорости точек 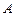 и
и 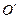 соответственно. Допустим, что в данный момент времени скорость
соответственно. Допустим, что в данный момент времени скорость  точки
точки  равна нулю, тогда для этого момента времени
равна нулю, тогда для этого момента времени
 .
.
Отсюда видно, что скорость 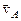 перпендикулярна вектору
перпендикулярна вектору 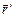 , т.е. направлена по касательной к окружности с центром в точке
, т.е. направлена по касательной к окружности с центром в точке  . Поскольку точка
. Поскольку точка 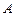 произвольная точка тела, это будет справедливо для любой точки тела.
произвольная точка тела, это будет справедливо для любой точки тела.
Таким образом, на основании этого можно сказать, что мгновенное распределение скоростей в теле в рассматриваемый момент времени будет в точности таким же, как и при вращении вокруг неподвижной оси, проходящей через точку  . Движение тела в этом случае называют мгновенным вращением. Прямая, проходящая через точку тела, скорость которой в данный момент времени равна нулю, называют мгновенной осью вращения.
. Движение тела в этом случае называют мгновенным вращением. Прямая, проходящая через точку тела, скорость которой в данный момент времени равна нулю, называют мгновенной осью вращения.
Словом “мгновенная” подчеркивают, что это понятие служит для описания распределения скоростей только в какой-то заданный момент времени. В отличие от неподвижной оси, сохраняющей свое положение в теле и в пространстве, мгновенная ось, вообще говоря, перемещается и в теле и в пространстве. Мгновенная ось может проходить через точку, лежащую вне тела.
Покажем теперь, что в пределах тела или за его пределами всегда можно найти точку, скорость которой в данный момент времени в системе 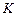 равна нулю. Скорость некоторой точки в системе
равна нулю. Скорость некоторой точки в системе 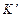 равна
равна 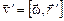 . Очевидно, что всегда можно подобрать такую величину и направление радиус-вектора
. Очевидно, что всегда можно подобрать такую величину и направление радиус-вектора 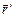 , чтобы выполнялось условие
, чтобы выполнялось условие 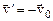 , т.е. чтобы в системе
, т.е. чтобы в системе 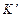 скорость этой точки по модулю была равна
скорость этой точки по модулю была равна  и направлена в сторону противоположную направлению вектора
и направлена в сторону противоположную направлению вектора  . В этом случае, как следует из уравнения (4), скорость этой точки в системе
. В этом случае, как следует из уравнения (4), скорость этой точки в системе 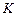 будет равна нулю.
будет равна нулю.
Мгновенная ось служит для описания мгновенного распределения только скоростей.
Для нахождения ускорений можно, например, воспользоваться формулой (4)
 ,
,
где  – ускорение системы отсчета
– ускорение системы отсчета 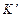 относительно системы
относительно системы 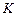 ,
, 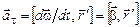 – тангенциальное, а
– тангенциальное, а  – нормальное ускорения точки
– нормальное ускорения точки 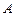 в системе
в системе 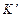 (см. раздел “Кинематика материальной точки”).
(см. раздел “Кинематика материальной точки”).
Вопросы для самоконтроля
 1. Угол поворота твердого тела, вращающегося вокруг неподвижной оси, меняется со временем по закону
1. Угол поворота твердого тела, вращающегося вокруг неподвижной оси, меняется со временем по закону 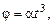 где
где 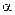 – положительная постоянная. Угловое ускорение равно:
– положительная постоянная. Угловое ускорение равно:
а) 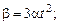 б)
б) 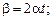
в) 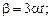 г)
г) 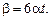
2. Твердое тело начинает вращаться вокруг неподвижной оси. Направление вращения показано на рис. 3. Вектор полного ускорения  некоторой точки
некоторой точки 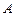 тела, отстоящей от оси вращения на расстоянии
тела, отстоящей от оси вращения на расстоянии  изменяется со временем по закону
изменяется со временем по закону 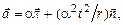 где
где 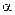 – положительная постоянная,
– положительная постоянная,  и
и  – единичные векторы, жестко связанные с точкой
– единичные векторы, жестко связанные с точкой 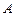 , направления которых показаны на рис. 3. Укажите правильные равенства:
, направления которых показаны на рис. 3. Укажите правильные равенства:
а)  б)
б)  в)
в) 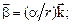
г) 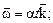 д)
д) 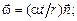 е)
е) 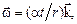
где  и
и 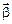 – векторы угловой скорости и углового ускорения точки
– векторы угловой скорости и углового ускорения точки 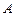 ,
,  – единичный вектор, направленный вдоль оси вращения.
– единичный вектор, направленный вдоль оси вращения.
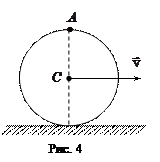 3. Колесо радиуса
3. Колесо радиуса 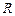 катится без проскальзывания по горизонтальной плоскости. Угловая скорость вращения колеса относительно оси, проходящей через точку
катится без проскальзывания по горизонтальной плоскости. Угловая скорость вращения колеса относительно оси, проходящей через точку 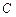 равна
равна  . Чему равна угловая скорость
. Чему равна угловая скорость 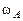 колеса относительно оси, проходящей через точку
колеса относительно оси, проходящей через точку 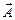 (см. рис. 4):
(см. рис. 4):
а)  б)
б) 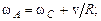
в)  г)
г)  ,
,
где 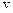 – скорость центра колеса.
– скорость центра колеса.
4. Твердое тело совершает плоское движение. Известны направления скоростей двух точек 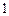 и
и  тела в некоторый момент времени. Какая из точек
тела в некоторый момент времени. Какая из точек 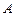 ,
, 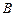 ,
, 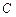 или
или 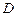 (см. рис. 5) лежит на мгновенной оси вращения.
(см. рис. 5) лежит на мгновенной оси вращения.
 |
Дата добавления: 2015-04-15; просмотров: 271; Мы поможем в написании вашей работы!; Нарушение авторских прав |