Задачи для самостоятельного решения. Задача 1.Колесо вращается вокруг неподвижной оси так, что угол его поворота зависит от времени как

Задача 1.Колесо вращается вокруг неподвижной оси так, что угол 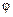его поворота зависит от времени как , где 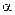– положительная постоянная. Найти полное ускорение точки 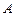на ободе колеса в

тот момент времени , когда скорость этой точки равна .

О т в е т. .

Задача 2.Твердое тело вращается, замедляясь вокруг неподвижной оси с угловым ускорением , где 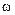– его угловая скорость. Найти среднюю угловую скорость тела за время, в течении которого оно будет вращаться, если в начальный момент времени его угловая скорость равна .

О т в е т. .

Задача 3.Твердое тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворота 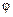по закону , где и – положительные постоянные. В момент времени угол . Найти зависимости от времени: а) угла поворота; б) угловой скорости.

О т в е т. а) ; б) .

Задача 4.Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением , где – постоянный вектор, 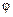– угол поворота из начального положения. Найти угловую скорость тела в зависимости от угла

О т в е т.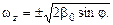

Задача 5.Твердое тело вращается с угловой скоростью где и – положительные постоянные, и – орты осе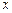й и Найти модули угловой скорости и углового ускорения в момент времени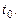

О т в е т.

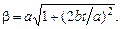
Задача 6.Колесо радиуса 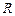(рис. 12) катится без скольжения по горизонтальной поверхности со скоростью 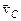. Найти скорости точек колеса 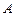и 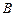, которые расположены на расстоянии ( < 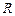) от центра колеса.

О т в е т. , .

Задача 7.Шар радиуса 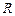катится без скольжения по горизонтальной плоскости так, что его центр движется с постоянным ускорением Через время после начала движения его положение соответствует положению, изображенному на рис. 13. Найти ускорения точек 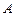и .

Задача 8.Вращающийся диск (рис. 10) движется в положительном направлении оси 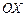. Найти уравнение 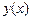, характеризующее положение мгновенной оси вращения, если в начальный момент ось 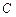диска находилась в точке и в дальнейшем движется с постоянным ускорением (без начальной скорости), а диск вращается с постоянной угловой скоростью .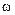

О т в е т. .

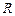Задача 9.Цилиндр катитсябез скольжения по горизонтальной плоскости. Радиус цилиндра равен Найти радиусы кривизны траекторий точек 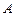и 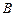(см. рис. 13).

О т в е т.

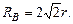
Задача 10.Круглый конус с углом полураствора и радиусом см катится без скольжения по горизонтальной плоскости, как показано на рис. 14. Вершина конуса закреплена шарнирно в точке которая находится на одном уровне с точкой 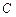– центром основания конуса. Скорость точки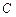 Найти модули: а) угловой скорости конуса; б) углового ускорения конуса.

О т в е т. а) ; .