
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Умеренные интенсивности.
Последовательность процессов отражена в таблице 1 .
При поглощении лазерного излучения частица нагревается. Это приводит к нагреву окружающей жидкости и, соответственно, к изменению ее показателя преломления, однако этот процесс не приводит к существенному изменению пропускания, поэтому в соответствующей графе таблицы стоит прочерк. Существенное изменение пропускания начинается после вскипания жидкости вокруг углеродной частицы и образования парового пузыря, т.к. в данном случае показатель преломления меняется скачкообразно, что приводит к нелинейному рассеянию на образовавшейся структуре. С ростом паровой прослойки нелинейное рассеяние увеличивается. Дальнейший нагрев частицы приводит к ее сублимации, и образованию пузырька углеродного пара, также растущего со временем. Это приводит к еще большему снижению пропускания.
Таблица 1. Последовательность процессов, происходящих в суспензиях углеродных наночастиц при умеренных интенсивностях облучения.
| № | Процесс | Результат процесса, приводящий к изменению пропускания |
| Нагрев углеродной частицы | - |
| Изменение показателя преломления жидкости | - |
| Вскипание жидкости вокруг частицы | Нелинейное рассеяние на пузырьке пара жидкости |
| Сублимация углеродной частицы | Нелинейное рассеяние на пузырьке углеродного пара |
В [1] измерен спектральный состав вспышки, возникающей при облучении суспензии длиной волны 1.06 мкм при плотности энергии до 20 Дж/см2 и длительности импульса 10 нс. Получен непрерывный спектр излучения абсолютно черного тела в котором отсутствуют линии, соответствующие ионам углерода. В данной работе сделан вывод, что при таких плотностях энергии (до 20 Дж/см2) лимитинг может быть объяснен механизмом роста пузырьков пара и углерода без привлечения механизма ионизации.В [2,3] впервые проведено теоретическое исследование и компьютерное моделирование этого процесса. Ниже коротко представлены основные результаты этих исследований.
Углеродная частица поглощает интенсивное лазерное излучение, что приводит к ее нагреву и нагреву окружающей жидкости. Высокая скорость нагрева приводит к тому, что окружающая частицу жидкость глубоко заходит в метастабильное состояние вплоть до температуры взрывного кипения [4]. Происходит взрывное испарение тех объемов жидкости, которые глубоко зашли в метастабильное состояние. Давление в образовавшейся паровой оболочке равно давлению насыщенного пара, которое соответствует температуре взрывного вскипания. Это давление намного превышает внешнее, и паровая оболочка начинает расширяться до тех пор, пока давление в ней не будет равно внешнему, т.е. атмосферному давлению. Рассеяние света на расширяющейся паровой оболочке приводит к нелинейному ограничению излучения. С увеличением плотности входной энергии частица нагревается быстрее, т.е. порог ограничения уменьшается, но размер области, зашедшей в метастабильное состояние, также уменьшается, поэтому пузырь может расшириться до меньших размеров. В пределе размер пузыря становится столь мал, что его образование уже не как не сказывается на пропускании. Но при этом плотности энергии уже становятся достаточны для сублимации углеродной частицы и, возможно, ионизации углеродного пара. Эти процессы будут подробно рассмотрены в следующем разделе. В данном разделе рассмотрение проводится при умеренных плотностях входной энергии, недостаточных для нагрева частицы до температуры сублимации углерода (3770 К).
Для численного моделирования нелинейного оптического ограничения света суспензией углеродных частиц были самосогласованно решены три задачи:
0. Задача газодинамики образования и роста паровой оболочки на нагретой частице.
1. Задача рассеяния на образовавшемся паровом пузырьке, окружающем частицу.
2. Задача прохождения излучения через среду.
Определение радиального распределения температуры в системе углеродная частица - паровая оболочка находится из решения системы уравнений теплопроводности для частицы, паровой оболочки и воды с движущимися граничными условиями. Скорость роста паровой оболочки, вызванная перепадом давлений, определялась из решения уравнения Плессета-Цвика [2-4], скорость испарения-конденсации рассчитывалась из уравнения Герца-Кнудсена [2-4].
До образования паровой прослойки расчет сечений рассеяния - поглощения углеродной частицы представляет собой задачу рассеяния излучения однородным шаром и рассчитывается в соответствии с теорией Ми. Рассеяние излучения на образовавшихся вокруг частиц паровых оболочках сводится к задаче рассеяния излучения на шаре с оболочкой. Для использования алгоритма Ми в этом случае концентрическая сфера заменялась однородным шаром с единым эффективным показателем преломления. На рис. 1 приведена зависимость сечений рассеяния-поглощения от радиуса паровой оболочки. Видно, что с увеличением радиуса паровой оболочки сечение поглощения падает (за исключением небольшого максимума в самом начале), тогда как сечение рассеяния резко растет. Поэтому светоиндуцированное рассеяние играет основную роль в процессе нелинейного оптического ограничения суспензиями углеродных частиц.
Для определения оптического ограничения решалась задача прохождения излучения через протяженную среду. Среда заменялась набором амплитудных экранов, на каждом из которых рассчитывались радиус и плотность паровых оболочек, образовавшихся вокруг частиц, рассеяние и поглощение на этих двухслойных комплексах, вычислялся коэффициент поглощения как функция продольной (вдоль направления распространения света) координаты и выходная интенсивность.
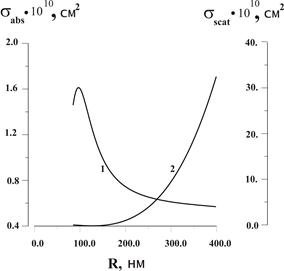
Рис.1. Зависимость сечений поглощения (1) и рассеяния (2) от радиуса паровой оболочки. Расчет проведен в рамках теории Ми с эффективным показателем преломления, рассчитанным по формуле Браггемана. Длина волны падающего излучения – 1064 нм.
На рис. 2 приведены результаты численного моделирования начальной стадии нелинейного процесса в видимом и ближней ИК-областях спектра. Исследовались водные суспензии углеродных частиц со средним радиусом частиц 80 нм. Расчет проведен для плотности входной энергии 0.2 Дж/см2, - при данной плотности энергии на длине волны 532 нм (2-я гармоника Nd:YAG лазера) наблюдается снижение пропускания в 2 раза. Видно, что в ближней ИК-области эффективность ограничения падает, что связано с увеличением линейного поглощения воды в этой области.

Рис.2. Зависимость пропускания водной углеродной суспензии от длины волны падающего излучения. Радиус углеродной частицы – 85 нм. Длительность импульса – 10 нс. Длина кюветы – 3 мм. Плотность падающей энергии – 0.2 Дж/см2. Пунктирная линия – линейное пропускание (рассчитывается из закона Бугера), сплошная линия – нелинейное пропускание (результат численного моделирования.)
Дата добавления: 2015-04-15; просмотров: 219; Мы поможем в написании вашей работы!; Нарушение авторских прав |