
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Схема 3.1
Коэффициенты Стьюдента t
| Число вариант n | Число степеней свободы f=n-1 | Значения t при Р | ||
| 0,90 | 0,95 | 0,99 | ||
| 6,314 | 12,71 | 65,66 | ||
| 2,920 | 4,303 | 9,925 | ||
| 2,353 | 3,182 | 5,841 | ||
| 2,132 | 2,776 | 4,604 | ||
| 2,015 | 2,571 | 4,034 | ||
| 1,94 | 3,71 | |||
| 1,90 | 2,37 | 3,50 | ||
| 1,86 | 2,31 | 3,36 | ||
| 1,83 | 2,26 | 3,25 | ||
| 1,81 | 2,23 | 3,17 | ||
| 1,75 | 2,13 | 2,95 | ||
| 1,73 | 2,09 | 2,85 |
Таблица 3.2
Табличные коэффициенты QT
| Число вариант n | Значения QТ при Р | ||
| 0,90 | 0,95 | 0,99 | |
| 0,94 | 0,98 | 0,99 | |
| 0,76 | 0,85 | 0,93 | |
| 0,64 | 0,73 | 0,82 | |
| 0,56 | 0,64 | 0,74 | |
| 0,51 | 0,59 | 0,68 | |
| 0,47 | 0,54 | 0,63 | |
| 0,44 | 0,51 | 0,60 | |
| 0,41 | 0,48 | 0,57 |
Пример 3.3. Оцените наличие промахов в выборке результатов, приведенных в примере 8.1.
Решение. 1. Располагают результаты выборки в порядке их возрастания и определяют диапазон выборки:
0,2015; 0,2020; 0,2031; 0,2033; 0,2048;
ω= 0,2048-0,2015 = 0,0033.
2. Поскольку в данной выборке п > 3, проверяем на промах наибольшую варианту по уравнению (3.11):
Qр = (0,2048 - 0,2033)/0,0033 = 0,45.
3. Согласно таблице 3.2, при Р = 0,95 в случае п = 5 QТ = 0,73.
Так как 0,45 < 0,73 или Qр < QТ то проверяемое значение не является промахом. Следовательно, промахи в данной выборке отсутствуют.
Схема 3.1
1.Сравнивают значения дисперсий рассматриваемых выборок, определяют расчетное значение F-критерия по уравнению:
F =S12/S22 (3.12)
где Fp — расчетная величина критерия; S12 — большая по значению дисперсия; S22 — меньшая дисперсия.
2. По табл. 3.3, с учетом числа вариант рассматриваемых выборок п1 и п2 (соответственно числа степеней свободы: f1 = n1-1, f2= п2-1), для соответствующей вероятности Р определяют теоретическое значение F-критерия: FT.
Таблица 3.3
Теоретические значения критерия Фишера (FT)
| f2(f2=n2-1) | Значения F1 при f1(f1=n1-1) | ||||
| P=0.95 | |||||
| 19.00 | 19.16 | 19.25 | 19.30 | 19.33 | |
| 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | |
| 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | |
| 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | |
| 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | |
| P=0.99 | |||||
| 99.00 | 99.17 | 99.25 | 99.25 | 99.30 | 99.33 |
| 30.81 | 29.46 | 28.71 | 28.71 | 28.24 | 27.91 |
| 18.00 | 16.69 | 15.98 | 15.98 | 15.32 | 15.21 |
| 13.27 | 12.06 | 11.39 | 11.39 | 10.97 | 10.67 |
| 10.92 | 9.78 | 9.15 | 9.15 | 8.75 | 8.47 |
3. Сопоставляют расчетную и теоретическую величины F-критерия, делают вывод о равнозначности рассматриваемых выборок.
Если рассчитанная величина Fp меньше табличного значения Ft (табл. 3.3), то сравниваемые выборки однородны, т. е. принадлежат одной генеральной совокупности (в противном случае средние арифметические 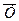 рассматриваемых выборок сравнивать между собой нельзя).
рассматриваемых выборок сравнивать между собой нельзя).
4. Определяют средневзвешенную дисперсию данных выборок (  ):
):
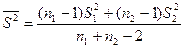 (3-13)
(3-13)
где индекс 1 относится к числу вариант (п) и дисперсии (S) первой выборки, индекс 2 — соответственно ко второй.
5. Оценивают_статистическую неразличимость средних арифметических величин  и
и  при помощи t- критерия по уравнению:
при помощи t- критерия по уравнению:

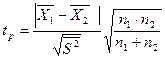 (3.14)
(3.14)
где tp — расчетная величина t-критерия; п1 и пг — число вариант выборки соответственно с дисперсией S12 и S22.
6. Расчетное значение t-критерия сравнивают с теоретическим (tT), определенным по табл. 3.1 для выбранного уровня доверительной вероятности Р и числа степеней свободы, равного f= (n1 + пг - 2). Если tp < tT то значимого различия между двумя 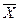 не существует, т. е. при условиях сравниваемых выборок систематическая погрешность отсутствует.
не существует, т. е. при условиях сравниваемых выборок систематическая погрешность отсутствует.
Пример 3.4. При кислотно-основном титровании аликвотных частей того же раствора соды, что и в примере 3.1, но выполненном с применением нового индикатора, была получена выборка результатов (в граммах): 0,2030; 0,2038; 0,2039; 0,2050. Оцените статистическую однородность стандартных отклонений обеих выборок и их средних арифметических значений, если применение Q-теста ко вновь полученной выборке показало, что промахи в ней отсутствуют, а рассчитанные ее метрологические характеристики следующие:  = 0,2039;
= 0,2039;  =67,7 .10-8.
=67,7 .10-8.
Решение. Согласно схеме 3.1:
1. Сравнив значения дисперсий рассматриваемых выборок, определяют расчетное значение F-критерия:
Первая выборка результатов: n1=5; X1=0,2029; 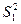 = 164,5 . 10-8 (см. пример 3.1).
= 164,5 . 10-8 (см. пример 3.1).
Вторая выборка: n2 =4;  = 0,2039;
= 0,2039;  =67,7.10-8. Так как
=67,7.10-8. Так как 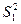 >
>  , в числитель уравнения (3.12) F-критерия следует поместить значение дисперсии первой выборки результатов:
, в числитель уравнения (3.12) F-критерия следует поместить значение дисперсии первой выборки результатов:
Fp= 164,5.10-8/(67,7-10-8) = 2,43.
2. По табл. 3.3 с учетом n1 = 5, а п2 = 4 (соответственноf1 = 4, f2 = 3) для Р= 0,95 определяют теоретическое значение F-критерия: FT= 9,12.
3. Поскольку 2,43 < 9,12 или Fp < FT, расхождение между дисперсиями данных выборок незначительно, следовательно, обе выборки равнозначны.
4. Определяем средневзвешенную дисперсию по уравнению (3.13):

5. Рассчитываем t-критерий по уравнению (3.14):

6. По табл. 3.1 для Р = 0,95 и f=5 + 4-2 = 7 находим tT = 2,37.
Так как 1,35 < 2,37 или tp < tT следовательно, значимого различия между рассматриваемыми величинами средних арифметических значений не существует. Таким образом, применение нового индикатора не приводит к систематическим погрешностям при титровании, т. е. к изменению точности результатов.
Выполнить задания
1. Погрешность метода 0,2%. Сколько значащих цифр следует указать в полученных в ходе анализа значениях: 20,452; 20,22; 0,48255?
2. При определении содержания свинца в сплаве были получены следующие результаты (%): 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,25; 14,19. Оцените наличие промахов, рассчитайте среднее арифметическое и доверительный интервал.
3. Определите, является ли последний результат промахом:
• При анализе получены следующие данные о содержании в топазе А1203(%): 53,96; 54,15; 54,05; 54,08 54,32.
• При анализе получены данные о содержании в апатите Р205.(%): 35,11; 35,14; 35,18; 35,21; 35,42.
• При определении гравиметрическим методом сульфат-иона получены следующие данные о содержании S03(%): 15,51; 15,45; 15,48; 15,53; 16,21.
4. Вычислите стандартное отклонение единичного определения и доверительный интервал среднего значения для Р = 0,95:
• При определении ванадия получены следующие результаты (в граммах): 8,00 .10-4; 8,40 .10-4.
• В серебряной монете при анализе параллельных проб получено следующее содержание серебра (%): 90,04; 90,12; 89,92; 89,94; 90,08; 90,02.
• При определении сурьмы в сплаве титриметрическим методом получены данные (%): 11,95; 12,03; 11,98; 12,04.
• При определении концентрации перманганата калия тремя студентами получены следующие результаты (моль/л): 0,1013; 0,1012; 0,1012; 0,1014;
0,1015; 0,1012; 0,1012; 0,1013; 0,1013; 0,1015; 0,1015; 0,1013.
5. Статистически значимо ли различаются результаты приведенных методов анализа:
• Массовую долю (%) СuО в минерале определили методом иодометрии и методом комплексонометрии. По первому методу получили результаты: 38,20; 38,00; 37,66. По второму: 37,70; 37,65; 37,55.
• Содержание Fe203 в руде определили перманганатометрическим методом и методом комплексонометрии. При этом получили следующие результаты (%): а) 60,12; 61,00; 61,25; б) 58,75; 58,90; 59,50.
Творческие задания
1. При анализе стандартного образца, содержащего 1,47% Ag, были получены следующие результаты (%): 1,31; 1,45; 1,42; 1,32; 1,30. Определите стандартное отклонение, доверительный интервал, сделайте выводы о возможности систематической погрешности в использованном методе определения серебра.
2. Имеется ли систематическая погрешность в определении платины новым методом, если при анализе стандартного образца платиновой руды, содержащего 85,97% Pt, были получены следующие результаты содержания платины (%): 85,97; 85,71; 85,84; 85,79.
3. Определите, существует ли значимое различие между выборочным средним значением при определении массовой доли (%) серы в каменном угле: 2,10; 2,12; 2,13; 2,15; 2,15 и средним генеральной совокупности µ = 2,15% для п = 80.
4. Содержание активного хлора в хлорной извести составляет (%): 37,11; 37,18; 37,23; 37,15. Среднее значение генеральной совокупности (п = 50) 37,02. Установите, существует ли значимое различие между выборочным средним и средним генеральной совокупности.
5. При определении ванадия получены два результата (в граммах): 8,00 • 10 -4; 8,40 • 10-4. Сколько параллельных определений необходимо провести для достижения доверительного интервала ±0,41 . 10-4? Оправдано ли применение этого метода для достижения такого доверительного интервала?
6. При анализе стали получили следующее содержание марганца: 48,35 и 48,00%. Установите, сколько параллельных проб необходимо для определения марганца с доверительным интервалом ± 0,48?
Занятие 2
Пример 4.1.Вычислите рН 0,01 М раствора аммиака. КNH3 =1,76-10-5.
Решение. В водном растворе аммиака имеет место равновесие: NH3+H20 ↔NH4+ + OH- следовательно, согласно табл. 4.1, в растворе слабого основания
pH = 14 + lg 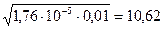
Дата добавления: 2015-04-15; просмотров: 1609; Мы поможем в написании вашей работы!; Нарушение авторских прав |