ОПРЕДЕЛЕНИЕ СИЛЫ И ЦЕНТРА ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКИЕ ФИГУРЫ

Задача определения результирующей силы гидростатического давления на плоскую фигуру сводится к нахождению величины этой силы и точки ее приложения или центра давления. Представим резервуар, наполненный жидкостью и имеющий наклонную плоскую стенку (рис. 1.12).

На стенке резервуара наметим некоторую плоскую фигуру любого очертания площадью w. Координатные оси выберем так, как указано на чертеже. Ось z перпендикулярна к плоскости чертежа. В плоскости уz расположена рассматриваемая фигура, которая проектируется в виде прямой, обозначенной жирной линией, справа показана эта фигура в совмещении с плоскостью уz.

В соответствии с 1-м свойством гидростатического давления можно утверждать, что во всех точках площади w давление жидкости направлено нормально к стенке. Отсюда заключаем, что сила гидростатического давления, действующая на произвольную плоскую фигуру, также направлена нормально к ее поверхности.

Рис. 1.12. Давление жидкости на плоскую стенку

Для определения силы давления выделим элементарную (бесконечно малую) площадку dw. Силу давления dP на элементарную площадку определим так:

dP = pdw = (p₀ + rgh)dw,

где h - глубина погружения площадки dw.

Так как h = ysina, то dP =pdw = (p₀ + rgysina)dw.

Сила давления на всю площадку w:

. (1.44)

Первый интеграл представляет собой площадь фигуры w:

.

Второй интеграл представляет собой статический момент площадки w относительно оси х. Как известно, статический момент фигуры относительно оси х равен произведению площади фигуры w на расстояние от оси х до центра тяжести фигуры, т.е.

.

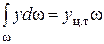Подставляя в уравнение (1.44) значения интегралов, получаем

P = p_ow + rgsinay_ц.тw.

Но так как y_ц.т sina = h _ц.т - глубина погружения центра тяжести фигуры, то:

P = (p₀ + rgh_ц.т)w. (1.45)

Выражение, заключенное в скобки, представляет собой давление в центре тяжести фигуры:

p₀ + rgh_ц.т = p_ц.т .

Следовательно, уравнение (1.45) можно записать в виде

P = p_ц.т w. (1.46)

Таким образом, сила гидростатического давления на плоскую фигуру равна гидростатическому давлению в центре тяжести ее, умноженному на величину площади этой фигуры. Определим центр давления, т.е. точку приложения силы давления Р. Так как поверхностное давление , передаваясь через жидкость, равномерно распределяется по рассматриваемой площади, то точка приложения силы w будет совпадать с центром тяжести фигуры. Если над свободной поверхностью жидкости давление атмосферное (p₀ = p_атм), то его учитывать не надо.

Давление, обусловленное весом жидкости, неравномерно распределяется по площади фигуры: чем глубже расположена точка фигуры, тем большее давление она испытывает. Поэтому точка приложения силы
P = rgh_ц.тw будет лежать ниже центра тяжести фигуры. Координату этой точки обозначим y_ц.д. Для ее нахождения воспользуемся известным положением теоретической механики: сумма моментов составляющих элементарных сил относительно оси х равна моменту равнодействующей силы Р относительно той же оси х, т.e.

,

так как dP = rghdw = rgysinadw, то

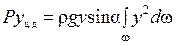. (1.47)

Здесь значение интеграла представляет собой момент инерции фигуры относительно оси х:

,

а сила .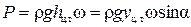

Подставляя эти соотношения в уравнение (1.47), получаем

y_ц.д = J_x / y_ц.тw. (1.48)

Формулу (1.48) можно преобразовать, воспользовавшись тем, что момент инерции J_x относительно произвольной оси х равен

J_x = J₀ + y²_ц.тw, (1.49)

где J₀ - момент инерции площади фигуры относительно оси, проходящей через ее центр тяжести и параллельной оси х; y_ц.т - координата центра тяжести фигуры (т.е. расстояние между осями).

С учетом формулы (1.49) получим: . (1.50)

Уравнение (1.50) показывает, что центр давления, обусловленный весовым давлением жидкости, всегда расположен ниже центра тяжести рассматриваемой фигуры на величину 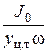и погружен на глубину

, (1.51)

где h_ц.д = y_ц.д sina - глубина погружения центра давления.

Мы ограничились определением только одной координаты центра давления. Этого достаточно, если фигура обладает симметрией относительно оси у, проходящей через центр тяжести. В общем случае надо определять и вторую координату. Методика ее определения такая же, как и в рассмотренном выше случае.

Дата добавления: 2014-11-13; просмотров: 19; Нарушение авторских прав