ЭПЮРЫ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ. ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ СИЛЫ И ЦЕНТРА ДАВЛЕНИЯ

Эпюрой называется графическое изображение распределения гидростатического давления в плоскости рассматриваемой поверхности, выполненное в определенном масштабе.

Для построения эпюры воспользуемся уравнением распределения давления в покоящейся жидкости:

p = rgh.

С геометрической точки зрения эта формула представляет собой уравнение прямой линии. Для построения прямой линии достаточно знать положение двух ее точек. В точке А, например, давление на плоскую фигуру равно нулю, так как h = 0 (рис.1.13). В точке В давление равно rgH. Давление нормально к поверхности. Отложим перпендикулярно к плоскости фигуры вектор ЕВ, равный rgH. Тогда, соединив точки А и Е прямой, получим графическое изображение распределения гидростатического давления на плоскую фигуру в виде прямоугольного треугольника.

Рис. 1.13. Эпюра гидростатического давления

на вертикальную плоскую поверхность

Предположим, что ширина фигуры (размер, перпендикулярный плоскости чертежа, см. рис. 1.13) равна b. Тогда сила давления на плоскую фигуру равна:

;

,

где W - площадь эпюры.

Следовательно, сила давления равна площади эпюры давления, умноженной на ширину поверхности, т.е.

, (1.52)

или в общем случае сила гидростатического давления равна объему эпюры давления. Сила давления Р перпендикулярна к рассматриваемой поверхности АВ и проходит через центр тяжести эпюры давления.Это следует из самого понятия центра тяжести как точки приложения равнодействующей всех элементарных сил данной силовой фигуры (Р - равнодействующая всех элементарных сил давления). Таким образом, для определения силы и центра давления графическим способом необходимо:

1. Построить эпюру давления.

2. Определить площадь эпюры давления.

3. Определить силу давления, которая равна площади эпюры, умноженной на ширину поверхности, т.е. объему эпюры давления.

4. Определить центр тяжести эпюры давления.

5. Сила давления проходит через центр тяжести эпюры и направлена по нормали к поверхности. Точка пересечения вектора Р и поверхности - центр давления.

1.10. ОПРЕДЕЛЕНИЕ СИЛЫ И ЦЕНТРА ДАВЛЕНИЯ ЖИДКОСТИ
НА КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ

На практике приходится определять силу гидростатического давления не только на плоские, но и на криволинейные поверхности. Рассмотрим частный случай криволинейной поверхности - цилиндрическую, т.е. поверхность, которая проектируется на нормальную к ней плоскость в одну кривую линию. Этот случай наиболее часто встречается на практике.

Будем полагать, что давление над свободной поверхностью жидкости и с правой стороны от криволинейной поверхности одинаковое и равное, например, атмосферному. Тогда результирующая сила давления определится избыточным давлением со стороны жидкости, т.е. ее весовым давлением.

Выделим на некоторой цилиндрической поверхности АВ (рис. 1.14) элементарную площадку dw, погруженную на глубину у. Сила давления dP всегда направлена нормально к площадке dw.

Рис.1.14. Давление жидкости на криволинейную поверхность

Элементарная сила dP избыточного гидростатического давления на площадку dw равна:

dP = rgydw,

где у - глубина погружения площадки dw.

Разложим dP на вертикальную и горизонтальную составляющие, обозначив угол отклонения линий ее действия от горизонтали a:

Произведения cosa dw и sina dw равны площадям проекций элементарной площадки соответственно на вертикальную (уz) и горизонтальную (хz) плоскости, т.е.

cosa dw = dw_y;

sina dw = dw_x ,

тогда dP_x = rgy dw_y ;

dP_y = rgy dw_x .

Горизонтальная и вертикальная составляющие результирующей силы давления на рассматриваемую криволинейную поверхность будут равны:

; (1.53)

. (1.54)

Интеграл представляет собой статический момент площадки проекции цилиндрической поверхности АВ на вертикальную плоскость уz относительно оси х. В соответствии с предыдущим разделом имеем:

, (1.55)

где h_ц.т - глубина погружения центра тяжести проекции поверхности АВ на вертикальную плоскость yz; - площадь проекции.

С учетом уравнения (1.55) соотношение (1.53) примет вид:

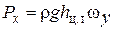, (1.56)

т.е. горизонтальная составляющая Р_x силы давления на криволинейную поверхность равна силе давления на проекцию w_у криволинейной поверхности на вертикальную плоскость.

Произведение yd представляет собой элементарный объем dW (см. рис. 1.14) и, следовательно, второй интеграл будет равен:

, (1.57)

где W - объем тела, ограниченного поверхностью АВ и ее проекциями на горизонтальную и вертикальную координатные плоскости. Это тело называется телом давления. С учетом уравнения (1.57) уравнение (1.54) можно записать так:

.

Таким образом, вертикальная составляющая силы давления жидкости на криволинейную поверхность равна весу жидкости в объеме тела давления:

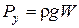. (1.58)

Результирующая сила давления Р определяется по правилу сложения векторов:

. (1.59)

Определим координату центра давления, т.е. точку приложения силы Р.

Уравнение для горизонтальной составляющей Р_х идентично уравнению для плоской поверхности w_у. Значит, горизонтальная составляющая Р_х (рис. 1.15) пройдет через центр тяжести эпюры давления на вертикальную проекцию криволинейной поверхности. Линия действия вертикальной составляющей силы давления Р_у должна проходить через центр тяжести тела давления W (см. рис. 1.15). Вектор силы давления должен пройти через точку пересечения Р_x и Р_y под углом a = arctg Р_x/Р_y к горизонту. Точка пересечения линий действия вектора Р с криволинейной поверхностью является центром давления.

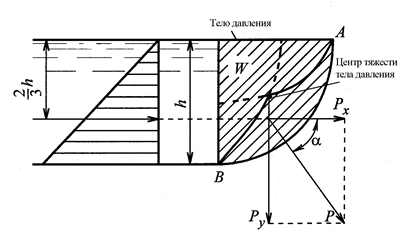
Рис. 1.15. Графическое определение центра давления

на криволинейную поверхность

Если рассмотреть силы, действующие на криволинейную поверхность (рис. 1.16), то, проведя рассуждения и выкладки точно так же, как и в предыдущем случае, можно показать, что величины Р_x и Р_y и их линии действия определяются по формулам (1.56), (1.58), (1.59), однако составляющая Р_y направлена вертикально вверх и равна взятому со знаком минус весу воображаемого жидкого тела с площадью сечения ЕАВСD. В первом случае имеем положительное, или мокрое, тело давления, а во втором - отрицательное, или сухое. Таким образом, если рассматриваемая криволинейная поверхность со стороны тела давления смачивается жидкостью, то Р_y направлено вниз по оси у, и если не смачивается, то вверх и как бы выталкивает криволинейную поверхность из воды.

Рис. 1.16. Сила давления на криволинейную поверхность обшивки понтона:
ц.т₁ - центр тяжести эпюры давления;

ц.т₂ - центр тяжести тела давления

Отметим, что плоская поверхность является частным случаем цилиндрической поверхности и сила и центр давления могут быть определены для нее рассмотренным выше способом.