ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ

В массе идеальной жидкости плотностью r, движущейся со скоростью v, выделим элементарный параллелепипед со сторонами dx, dy, dz
(см. рис. 1.6). На параллелепипед действуют массовые силы и поверхностные силы (силы давления). При этом в массовых силах можно выделить силы, которые действуют и на неподвижную жидкость (например, сила тяжести) и силу инерции, связанную с движением жидкости. При выводе дифференциальных уравнений гидростатики (см. гл. 1) было показано, что проекции массовых сил и сил давления на ось х соответственно равны

.

Проекция силы инерции на ось х определяется как произведение массы элементарного параллелепипеда на его ускорение, т.е.

.

В этом выражении v_x - проекция скорости v на ось х, t - время. Знак минус показывает, что сила инерции направлена в сторону, противоположную ускорению.

Уравнение равновесия будет иметь вид

(2.13)

или . (2.14)

Аналогичные уравнения получаются при проектировании сил на оси y и z.

Система дифференциальных уравнений движения идеальной жидкости имеет вид

,

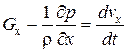, (2.15)

.

Эти уравнения позволяют определить изменение давления и скорости при изменении положения частиц струйки жидкости (координат x, y, z) и времени. Они были получены Л. Эйлером в 1755 г., поэтому их называют еще уравнениями Эйлера.