УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ

Преобразуем уравнение Эйлера. Так как все преобразования выполняются аналогично, то покажем их на примере первого уравнения системы (2.15). Умножим каждый член уравнения на dx. Получим

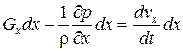. (2.16)

Воспользуемся понятием полного дифференциала, имея в виду, что компонента скорости v_x является функцией координат и времени.

Можно записать

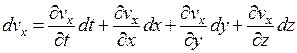, (2.17)

откуда, учитывая, что 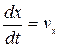, имеем

.

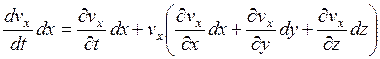Для установившегося движения .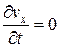

Тогда уравнение (2.17) принимает вид

. (2.18)

Так как для установившегося движения компонента скорости v_x не зависит от времени, то выражение в скобках уравнения (2.18) является полным дифференциалом скорости v_x, т. е.

.

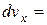
С учетом этого уравнение (2.18) может быть переписано так:

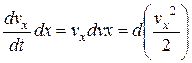. (2.19)

Тогда уравнение (2.16) принимает вид

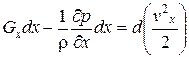. (2.20)

Следовательно, систему уравнений Эйлера (2.15) можно записать следующим образом:

,

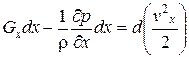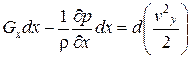, (2.21)

.

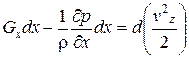Сложим левые и правые части уравнений (2.21)

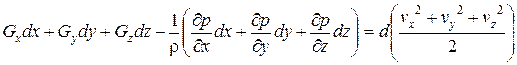. (2.22)

Давление р является функцией только координат, т. е. .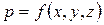

Тогда выражение в скобках в левой части уравнения (2.22) будет полным дифференциалом давления

.

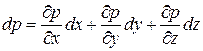Кроме того, известно, что .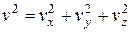

Тогда уравнение (2.22) принимает вид

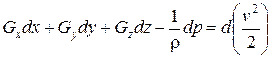. (2.23)

Если из массовых сил на жидкость действует только сила тяжести (действие сил инерции движущейся жидкости уже учтено в уравнении (2.23), то

; ; .

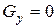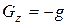Ускорение силы тяжести берется со знаком минус, так как оно направлено вертикально вниз, а положительное направление оси z - вверх. Тогда уравнение (2.23) (принимается, что r = const, т.е. жидкость считается несжимаемой) перепишется в виде

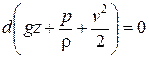. (2.24)

В результате интегрирования получается:

(2.25)

или 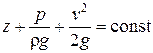. (2.26)

Уравнение (2.26) называется уравнением Бернулли для установившегося движения идеальной несжимаемой жидкости. Оно было получено академиком петербургской Академии наук Даниилом Бернулли в 1738 г. во время работы его в России и является одним из важнейших в гидравлике. Для двух сечений струйки жидкости уравнение (2.26) записывается в виде

. (2.27)