
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ГЕОМЕТРИЧЕСКИЙ И ЭНЕРГЕТИЧЕСКИЙ СМЫСЛ УРАВНЕНИЯ БЕРНУЛЛИ
Уравнение Бернулли (2.26) при v = 0 принимает вид
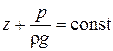 ,
,
т.е. переходит в основное уравнение гидростатики.
Таким образом, основное уравнение гидростатики является частным случаем уравнения Бернулли.
Определим размерность каждого члена уравнения Бернулли и его смысл. Первый член z имеет линейную размерность L и характеризует высоту положения струйки (потока) над горизонтальной плоскостью x0y. Таким образом, плоскость x0y является плоскостью сравнения. Величина z называется геометрической высотой положения или геометрическим напором.
Второй член p/rg также имеет линейную размерность:
 .
.
Он называется пьезометрической высотой или пьезометрическим напором, соответствующим давлению (абсолютному или избыточному).
Третий член уравнения v2/2g, как и предыдущие два, тоже имеет линейную размерность
 .
.
Он представляет собой высоту, на которую при отсутствии сопротивлений поднялся бы столб жидкости, начавший двигаться вертикально вверх со скоростью v. Поэтому этот член называется скоростной высотой или скоростным напором.
Таким образом, каждый член уравнения Бернулли можно представить в виде отрезка определенной длины. Отсюда вытекает геометрический смысл уравнения, который можно сформулировать так: для установившегося движения идеальной несжимаемой жидкости сумма трех высот - геометрической, пьезометрической и скоростной – есть величина постоянная или сумма трех напоров - геометрического, пьезометрического и скоростного – есть величина постоянная. Обозначим эту постоянную Н и назовем гидродинамическим напором. Если от горизонтальной плоскости вверх отложить геометрическую высоту, а затем пьезометрическую и скоростную (рис. 2.4) и соединить концы полученных отрезков по длине потока (струйки) жидкости, то получится горизонтальная линия, которая называется напорной. Если соединить концы отрезков z+p/rg, то получится пьезометрическая линия. Давление может браться абсолютным, но чаще всего принимается избыточным (манометрическим). Изменение пьезометрического напора, отнесенное к длине потока жидкости, на которой происходит это изменение, называется пьезометрическим уклоном.

Рис. 2.4. Иллюстрация уравнения Бернулли
Энергетический смысл уравнения Бернулли вытекает из того, что каждый член уравнения представляет собой удельную энергию, т.е. энергию, отнесенную к единице веса жидкости. Для того чтобы доказать это, рассмотрим, например, второй член уравнения p/rg. Размерность этого члена, как было показано выше, является линейной. С другой стороны, можно показать, что размерность этого члена является размерностью удельной энергии. Действительно,
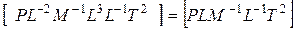 ,
,
и если воспользоваться, например, международной системой единиц измерения (СИ), то получается [Н×м/(кг×м×с2)] = [Дж/Н], т.е. единица измерения удельной энергии. Первый и третий члены уравнения Бернулли тоже должны иметь размерность удельной энергии. Таким образом, z - удельная потенциальная энергия положения, p/rg - удельная потенциальная энергия давления, v2/2g - удельная кинетическая энергия.
Энергетический смысл уравнения Бернулли для установившегося движения идеальной несжимаемой жидкости заключается в том, что сумма удельных потенциальных энергий положения и давления и удельной кинетической энергии есть величина постоянная. Очевидно, что уравнение является аналогом закона сохранения энергии.
Решение задач с использованием уравнения Бернулли выполняется в следующем порядке:
1) выбирается плоскость сравнения, т.е. плоскость, от которой отсчитывается величина z; плоскостью сравнения может служить любая горизонтальная плоскость;
2) принимаются два сечения по длине потока (струйки) жидкости, перпендикулярные направлению движения жидкости, причем второе сечение всегда должно быть после первого в направлении движения;
3) записывается уравнение Бернулли для двух сечений, заданные величины и искомая величина.
Для случая, когда из массовых сил на идеальную однородную жидкость действует только сила тяжести при установившемся движении, уравнение Бернулли можно вывести и менее громоздким методом, чем приведенный выше.
Рассмотрим участок элементарной струйки длиной dl (рис. 2.5) сечением dw. По длине струйки давление и скорость изменяются. На струйку действуют силы давления, тяжести и инерции.
Соответствующие составляющие, проектируемые на ось l, будут равны






Рис. 2.5. Элементарная струйка с действующими на нее силами
Знак минус в последнем выражении показывает, что сила инерции направлена в сторону, противоположную ускорению. Проекция силы тяжести положительна, так как она совпадает с направлением оси l, а проекция силы давления отрицательна, потому что в случае покоящейся жидкости эта сила должна уравновешивать силу тяжести. Уравнение равновесия будет иметь вид
 . (2.28)
. (2.28)
После сокращения на dl dw и деления каждого члена на r получим
 . (2.29)
. (2.29)
С учетом того, что  ,
,
а также cos α = - dz/dl, получим
 . (2.30)
. (2.30)
Отсюда  . (2.31)
. (2.31)
Выражение (2.31) можно переписать в виде
 . (2.32)
. (2.32)
После интегрирования и деления на g получается уравнение Бернулли для установившегося движения несжимаемой идеальной жидкости
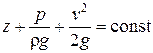 .
.
Дата добавления: 2014-11-13; просмотров: 1207; Мы поможем в написании вашей работы!; Нарушение авторских прав |