Линия тока. Элементарная струйка

В пространстве, занятом движущейся жидкостью, выделим в некоторый момент времени точку 1 (рис. 2.1), вектор скорости в которой v₁. В тот же момент времени в точке 2, бесконечно близкой к точке 1, вектор скорости v₂ и т.д. При бесконечно большом количестве точек огибающая всех этих векторов даст в пределе некоторую пространственную кривую, называемую линией тока. Таким образом, линия тока представляет собой кривую, в каждой точке которой в данный момент времени вектор скорости частицы жидкости касателен к этой кривой.

Рис. 2.1. Линия тока

Введем понятия установившегося и неустановившегося движения. В общем случае скорость жидкости зависит от координат x, y, z и времени t, т.е.

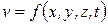. (2.1)

Если скорость жидкости в данной точке пространства, занятого движущейся жидкостью, не меняется со временем, то движение называется установившимся. В противном случае движение будет неустановившимся. Для неустановившегося движения справедливо соотношение (2.1), а для установившегося соотношение (2.2):

. (2.2)

Следует различать линию тока и траекторию движения частицы жидкости. Траектория представляет след движения одной частицы жидкости за некоторый отрезок времени. Линия же тока связывает между собой различные частицы и характеризует их движение в один и тот же момент времени. Линия тока и траектория движения частиц жидкости, на ней расположенных, совпадают только при установившемся движении.

На рис. 2.2 показано множество линий тока. Совокупность линий тока, проходящих через все точки элементарной площадки dw и перпендикулярно к ней, называется элементарной струйкой жидкости. Площадку dw называют живым сечением струйки.

Рис. 2.2. Элементарная струйка

Объем жидкости, протекающей за единицу времени через живое сечение, называется расходом элементарной струйки dQ. Отношение этого расхода к площади живого сечения dw называют местной скоростью движения v в данном сечении струйки. Таким образом,

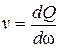, (2.3)

откуда . (2.4)