
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 5. Найти скорость и ускорение точки в любой момент времени, используя условие примера 2.
Найти скорость и ускорение точки в любой момент времени, используя условие примера 2.
Решение.Находим скорость:
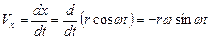 ,
, 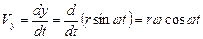 ,
,  ,
,
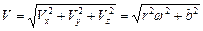 ,
,
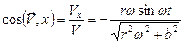 ,
, 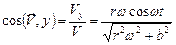 ,
, 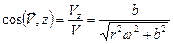
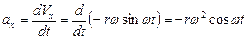 ,
, 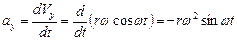 ,
,  ,
,
Находим ускорение: 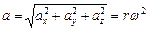 ,
,
 ,
, 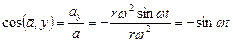
Ответ.  ,
, 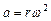 .
.
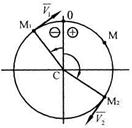 Пример 6.Точка движется по дуге окружности радиуса
Пример 6.Точка движется по дуге окружности радиуса 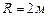 по закону
по закону  . Определить скорость точки в момент времени
. Определить скорость точки в момент времени  и
и 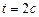 .
.
 Решение.Движение задано естественным способом. Примем за начало отсчета точку О, считая направление движения по часовой стрелке положительным. Находим дуговые координаты точки в заданные моменты времени:
Решение.Движение задано естественным способом. Примем за начало отсчета точку О, считая направление движения по часовой стрелке положительным. Находим дуговые координаты точки в заданные моменты времени:
 ,
,  .
.
Положение точек 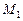 и
и 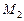 на траектории покажем с помощью углов (рис. 6):
на траектории покажем с помощью углов (рис. 6): 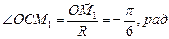 ,
, 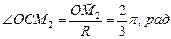 .
.
Находим величины скорости в заданные моменты времени:  ,
,
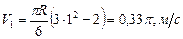 ,
,  . Так как
. Так как 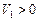 ,
, 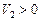 , то векторы скоростей будут направлены в сторону возрастания S по касательной к траектории (рис. 6).
, то векторы скоростей будут направлены в сторону возрастания S по касательной к траектории (рис. 6).
Ответ. 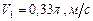 ,
,  .
.
Пример 8. 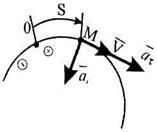 При отходе от станции поезд, двигаясь равноускоренно по закруглению радиуса 900 м, за время
При отходе от станции поезд, двигаясь равноускоренно по закруглению радиуса 900 м, за время  достиг скорости
достиг скорости 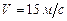 . Определить путь, пройденный поездом и его полное ускорение.
. Определить путь, пройденный поездом и его полное ускорение.
 Решение.За начало отсчета примем положение поезда в момент отхода от станции (рис. 7). Начальные условия движения:
Решение.За начало отсчета примем положение поезда в момент отхода от станции (рис. 7). Начальные условия движения:  ,
, 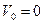 .
.
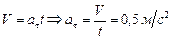 ,
,  ,
,  ,
,  .
.
Ответ. 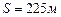 ,
, 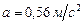
Пример 9.Поезд движется со скоростью  . При торможении ускорение равно
. При торможении ускорение равно 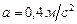 . Найти время и путь торможения.
. Найти время и путь торможения.
Решение. При начальных условиях движения имеем  ,
, 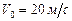 :
: 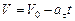 ,
, 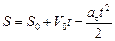 . Так как поезд остановился, то
. Так как поезд остановился, то  , тогда
, тогда  .
. 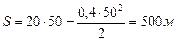 .
.
Ответ. 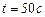 ,
, 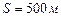 .
.
Пример 10.Определить ускорение точки через 2 с после начала движения из состояния покоя, если движение задано уравнениями:  ,
, 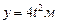 .
.
Решение. Находим проекции скорости и ускорения на координатные оси:
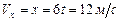 ,
,  ,
, 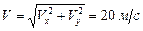 .
.  ,
,
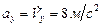 ,
, 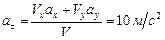 ,
,  ,
, 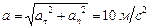 .
.
Ответ. 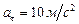 ,
, 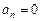 ,
, 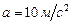
Пример 11.Перейти к естественному способу задания движения, если заданы уравнения движения точки в координатной форме: а)  , б)
, б) 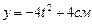 .
.
Решение.Для естественного способа задания необходимо знать:
1.  Траекторию.
Траекторию.
2.Закон движения.
3.Начало отсчета.
4.Положительное направление движения.
1. Траекторию движения определим, исключая время из уравнений движения а), б):
 из а)
из а) 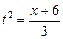 ; из б)
; из б) 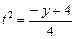 . Откуда получим
. Откуда получим  или
или 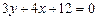 . Траектория представляет собой прямую линию (рис. 8), ограниченную точкой
. Траектория представляет собой прямую линию (рис. 8), ограниченную точкой 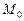 .
.
2. Закон движения находим по следующей формуле:  , где
, где 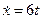 ,
, 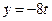 ,
, 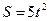 .
.
3. Начало отсчета находим из уравнений движения, подставив в них время, равное нулю:  ,
, 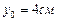 .
.
4. Положительное направление движения определим, подставив в уравнение движения время, равное 1с: 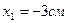 ,
,  .
.
Дата добавления: 2015-04-15; просмотров: 269; Мы поможем в написании вашей работы!; Нарушение авторских прав |