
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА 6. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ.

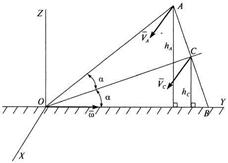 Пример 23.Конус с углом при вершине
Пример 23.Конус с углом при вершине 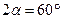 и радиусом основания
и радиусом основания  катится без проскальзывания по неподвижной горизонтальной поверхности. Определить скорость точки
катится без проскальзывания по неподвижной горизонтальной поверхности. Определить скорость точки  , если скорость центра основания постоянна и равна
, если скорость центра основания постоянна и равна  .
.
Решение.Движение конуса является сферическим. Мгновенная ось вращения конуса совпадает с образующей  , так как скорости точек образующей равны нулю (рис. 20).
, так как скорости точек образующей равны нулю (рис. 20).
Используя формулу (5), находим угловую скорость вращения конуса вокруг мгновенной оси вращения:  , где
, где  . Тогда
. Тогда  .
.
Вектор угловой скорости направлен по мгновенной оси вращения от точки  к точке
к точке  . Скорость точки
. Скорость точки  определим как вращательную скорость вокруг мгновенной оси вращения:
определим как вращательную скорость вокруг мгновенной оси вращения:  , где
, где  ;
;  .
.
Вектор скорости точки  направлен аналогично вектору скорости точки
направлен аналогично вектору скорости точки 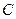 , т е. перпендикулярно плоскости
, т е. перпендикулярно плоскости 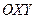 в соответствии с направлением угловой скорости вращения.
в соответствии с направлением угловой скорости вращения.
Ответ.  .
.
Пример 24. 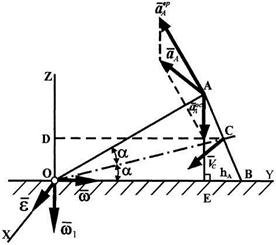 Используя условие примера 23, найти ускорение точки А.
Используя условие примера 23, найти ускорение точки А.
 Решение.Определим угловое ускорение конуса. При качении конуса по горизонтальной поверхности вектор угловой скорости будет вращаться вокруг вертикальной оси
Решение.Определим угловое ускорение конуса. При качении конуса по горизонтальной поверхности вектор угловой скорости будет вращаться вокруг вертикальной оси  .Так как модуль вектора угловой скорости постоянен, то конец вектора
.Так как модуль вектора угловой скорости постоянен, то конец вектора 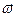 описывает окружность постоянного радиуса, равного модулю вектора угловой скорости в горизонтальной плоскости. Угловую скорость вращения вектора
описывает окружность постоянного радиуса, равного модулю вектора угловой скорости в горизонтальной плоскости. Угловую скорость вращения вектора 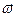 вокруг оси
вокруг оси  определяем, как угловую скорость вращения оси конуса вокруг оси
определяем, как угловую скорость вращения оси конуса вокруг оси  :
: 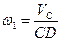 , где
, где  ,
,  . Вектор
. Вектор 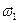 будет направлен противоположно положительному направлению оси
будет направлен противоположно положительному направлению оси  . Вектор углового ускорения
. Вектор углового ускорения  геометрически равен скорости конца вектора угловой скорости
геометрически равен скорости конца вектора угловой скорости 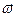 . Ее можно определить, как вращательную скорость точки, радиус вращения которой равен модулю угловой скорости
. Ее можно определить, как вращательную скорость точки, радиус вращения которой равен модулю угловой скорости  :
: 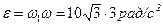 . Вектор углового ускорения будет находиться в плоскости
. Вектор углового ускорения будет находиться в плоскости 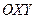 , приложен в неподвижной точке и направлен в сторону положительного направления оси
, приложен в неподвижной точке и направлен в сторону положительного направления оси  .
.
Ускорение точки в сферическом движении равно:  . По формулам (7), (8) находим
. По формулам (7), (8) находим  и
и  :
:  , где
, где  — отрезок перпендикуляра, опущенного из точки
— отрезок перпендикуляра, опущенного из точки  на вектор углового ускорения;
на вектор углового ускорения;  . Вектор
. Вектор  , перпендикулярный отрезку
, перпендикулярный отрезку  , находится в плоскости
, находится в плоскости  и направлен в соответствии с угловым ускорением, т. е. если смотреть с конца вектора
и направлен в соответствии с угловым ускорением, т. е. если смотреть с конца вектора  , то вектор
, то вектор  должен вращаться против хода часовой стрелки.
должен вращаться против хода часовой стрелки.
Вектор осестремительного ускорения  равен
равен  , где
, где 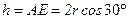 .
.  . Вектор
. Вектор  направлен по
направлен по 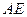 к мгновенной оси вращения:
к мгновенной оси вращения:
 ,
,  ,
,  .
.
Ответ.  .
.
Дата добавления: 2015-04-15; просмотров: 215; Мы поможем в написании вашей работы!; Нарушение авторских прав |