
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА 4. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

 Пример 15.Диск радиуса
Пример 15.Диск радиуса  вращается вокруг неподвижной оси по закону
вращается вокруг неподвижной оси по закону  . По ободу движется точка
. По ободу движется точка  по закону
по закону 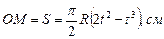 (рис. 12, а). Определить абсолютную скорость точки в момент времени
(рис. 12, а). Определить абсолютную скорость точки в момент времени  .
.
Решение.Точка  совершает сложное движение. Движение точки
совершает сложное движение. Движение точки  по ободу диска будет относительным, а движение диска — переносным. Абсолютную скорость точки
по ободу диска будет относительным, а движение диска — переносным. Абсолютную скорость точки  находим по формуле (1). Определим положение точки
находим по формуле (1). Определим положение точки  на траектории относительного движения. При
на траектории относительного движения. При 
 . Находим угол
. Находим угол 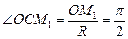 . Находим скорость относительного движения
. Находим скорость относительного движения  . При
. При 
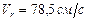 . Так как
. Так как  , то вектор
, то вектор  направлен по касательной к окружности в точке
направлен по касательной к окружности в точке  в сторону увеличения дуги
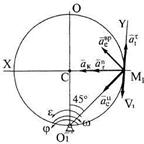
в сторону увеличения дуги  (рис.12). Находим скорость переносного движения
(рис.12). Находим скорость переносного движения  , где
, где  . При
. При 
 . Минус показывает, что направление
. Минус показывает, что направление  противоположно направлению положительного отсчета угла
противоположно направлению положительного отсчета угла  . Так как
. Так как  , то
, то  . Вектор
. Вектор  перпендикулярен вектору
перпендикулярен вектору  и направлен в соответствии с угловой скоростью (рис. 12, б). Так как
и направлен в соответствии с угловой скоростью (рис. 12, б). Так как  , тогда
, тогда  .
.
Ответ. 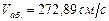 .
.
 Пример 16.Используя условие примера 15, определить абсолютное ускорение точки.
Пример 16.Используя условие примера 15, определить абсолютное ускорение точки.
 Решение.Центростремительное переносное ускорение
Решение.Центростремительное переносное ускорение  . Вращательное переносное ускорение
. Вращательное переносное ускорение  ,
,  . При
. При  ,
,  ,
,  .
.
Угловое ускорение направлено противоположно угловой скорости (рис. 13), так как производная имеет другой знак. Вектор 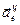 направлен по
направлен по  к оси переносного вращения. Вектор
к оси переносного вращения. Вектор  перпендикулярен
перпендикулярен  и направлен в соответствии с угловым ускорением.
и направлен в соответствии с угловым ускорением.
Тангенциальное относительное ускорение  .
.
При  ,
,  . Нормальное относительное ускорение
. Нормальное относительное ускорение 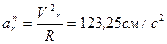 . Вектор
. Вектор  направлен по
направлен по  от точки
от точки  к точке
к точке 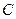 . Вектор
. Вектор  направлен противоположно вектору
направлен противоположно вектору  , так как
, так как  меньше нуля.
меньше нуля.
Находим ускорение Кориолиса:  ,
,  ,
,  .
.
Направление 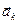 находим по правилу Жуковского. Так как вектор
находим по правилу Жуковского. Так как вектор  находится в плоскости, перпендикулярной переносной оси вращения, то повернем
находится в плоскости, перпендикулярной переносной оси вращения, то повернем  на 90° в направлении
на 90° в направлении  , т. е. по ходу часовой стрелки. Вектор
, т. е. по ходу часовой стрелки. Вектор 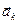 будет направлен от
будет направлен от  к
к 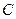 .
.
Спроектируем все найденные ускорения на выбранные координатные оси:  ,
,  ,
,  .
.
Ответ. 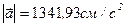
Дата добавления: 2015-04-15; просмотров: 223; Мы поможем в написании вашей работы!; Нарушение авторских прав |