
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
РАЗРАБОТКА КИНЕМАТИКИ БЕССТУПЕНЧАТОГО ПРИВОДА
В последнее время в станках все чаще используется привод с бесступенчатым регулированием. В некоторых старых конструкциях станков еще можно встретить бесступенчатый привод с использованием механических вариаторов, однако в современных станках применяют исключительно привод от бесступенчато регулируемых электродвигателей. Для изменения частоты вращения двигателя применяют различные устройства. Широкое применение находят сравнительно недавно разработанные частотные преобразователи, которые позволяют бесступенчато регулировать частоту вращения стандартных асинхронных электродвигателей с короткозамкнутым ротором.
Если диапазон частот вращения электродвигателя больше или равен требуемому диапазону регулирования привода, то можно передавать вращение от электродвигателя на шпиндель через одиночные передачи, не используя никаких переключаемых передач. В приводах подачи, где мощность относительно невелика, удается использовать регулируемый электродвигатель именно таким образом.
Вместе с тем, диапазон привода главного движения чаще всего оказывается больше, чем может обеспечить двигатель при выполнении всех требований к величинам крутящих моментов и мощности.
Если требуемый диапазон регулирования привода главного движения больше диапазона регулирования электродвигателя, то приходится последовательно с электродвигателем включать какую-либо ступенчатую коробку.
Если диапазон регулирования бесступенчатой части привода (например, электродвигателя) обозначить Rб, а диапазон регулирования подключаемой последовательно с ним коробки обозначить Rк, то очевидно, что диапазон регулирования привода в целом может быть получен таким образом:

На рис. 2.20 показано, как определяется соотношение между передаточными отношениями ступенчатой части (коробки) привода.

На рис. 3.1а) на вертикальной линии в произвольном логарифмическом масштабе отмечены две точки, соответствующие максимальной и минимальной частоте вращения бесступенчато регулируемого электродвигателя с диапазоном регулирования Rб. Включив после двигателя передачу с передаточным отношением i11, на ведомом валу можно получить частоты вращения, которые будут изменяться в таком же диапазоне от n1 до n1Rб.
Для увеличения диапазона регулирования привода можно вместо одиночной передачи i11 включить групповую передачу - i11 совместно с i21, как показано на рис. 3.1б). Понятно, что для того, чтобы можно было продолжать регулирование частот вращения далее, начиная с частоты n1Rб, нужно, чтобы соблюдалось соотношение:

Диапазон регулирования привода станет равным Rn= Rб2.
Если этого диапазона недостаточно, то можно включить в привод еще одну групповую передачу, например, i12 совместно с i22, как показано на рис. 3.1в). Из рисунка видно, что соотношение передаточных отношений в этой группе должно быть таким:

Первая групповая передача в данном случае играет роль основной группы, вторая – роль первой переборной. Легко заметить, что ступенчатая часть привода (ступенчатая коробка) должна иметь общие передаточные отношения, изменяющиеся по геометрическому ряду со знаменателем ряда 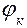 =Rб.
=Rб.
Надо, однако, иметь в виду, что номинальный паспортный диапазон регулирования двигателя всегда имеет некоторый допуск и может отклоняться от номинала в меньшую сторону. Если этого не учитывать, то на шкале частот вращения привода могут появляться “пробелы”, как показано на рис. 3.2а).

Для того, чтобы ни при каких условиях, из диапазона регулирования не была исключена какая-либо часть, значение знаменателя ряда передаточных отношений ступенчатой коробки несколько уменьшают путем умножения на коэффициент запаса, принимаемый обычно равным: а=(0,95…0,98). Если диапазон регулирования бесступенчатой части привода не уменьшится, то на шкале частот вращения появятся места, где возникает перекрытие – одни и те же частоты получаются с помощью разных передач как на рис. 3.2б). Однако если диапазон регулирования двигателя окажется меньше номинала или просто уменьшится за счет увеличения скольжения под влиянием нагрузки, то перекрытие пропадет, но шкала частот вращения останется непрерывной.
Если требуемый диапазон регулирования привода Rn задан, и если известен диапазон регулирования Rб бесступенчатой части привода, например, электродвигателя, то можно определить количество ступеней в ступенчатой части привода – коробке, встраиваемой в привод после двигателя.
Очевидно, что диапазон регулирования коробки будет
 ,
,
где  - знаменатель ряда передаточных отношений коробки, а Zк - число ступеней коробки.
- знаменатель ряда передаточных отношений коробки, а Zк - число ступеней коробки.
Учитывая, что диапазон регулирования привода равен произведению диапазонов регулирования бесступенчатой и ступенчатой части привода:
 ,
,
можно записать:
 .
.
Прологарифмировав это выражение, нужно решить его относительно Z:
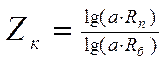 .
.
Полученное количество ступеней следует округлить до ближайшего большего целого значения.
Следует иметь в виду, что если диапазон регулирования бесступенчатой части привода больше, чем 2,83, то диапазон регулирования второй групповой передачи получится больше 8. Следовательно, уже после первой же групповой передачи придется использовать серии одиночных передач, т. е. применять сложенную структуру привода. Если же диапазон регулирования бесступенчатой части привода больше восьми, то в приводе вообще не удастся применить групповые передачи, и сразу после двигателя должны идти серии одиночных передач, общие передаточные отношения которых должны быть организованы таким образом, чтобы соотношение их было равно
 .
.
В качестве простейшего примера ниже рассмотрена разработка бесступенчатого привода при следующих исходных данных:
Минимальная частота вращения последнего вала привода (шпинделя) – 10 об/мин.
Максимальная частота вращения шпинделя – 2500 об/мин.
Минимальная частота вращения вала электродвигателя – 500 об/мин.
Максимальная частота вращения вала электродвигателя – 2050 об/мин.
Следовательно, диапазон регулирования электродвигателя (бесступенчатой части привода) будет
 .
.
А диапазон регулирования привода в целом

Если принять коэффициент запаса а=0,98, то число ступеней ступенчатой части привода (коробки) получится:
 .
.
Очевидно, следует принять
 и Zк=4.
и Zк=4.
Если принять структурную формулу привода
 ,
,
то во второй групповой передаче диапазон регулирования будет равен
 ,
,
что значительно больше восьми.
Следовательно, приходится принять сложенную структуру привода
 .
.
На рис 3.3 приведен вариант кинематической схемы и график частот вращения привода.
График построен следующим образом. Проведены вертикальные линии по числу валов. Поскольку привод бесступенчатый, горизонтальные линии можно было бы не проводить. Однако для построения необходима логарифмическая шкала, и нужно ориентироваться, где на этой шкале расположены точки, соответствующие определенным частотам вращения. Поэтому следует выполнить разметку шкалы частот вращения, приняв для этого любой стандартный геометрический ряд. В данном случае использована шкала с частотами из ряда с  =1,26. Это ни в коем случае не означает, что знаменатель ряда передаточных отношений привода равен 1,26. Просто использован такой масштаб. Если для шкалы взять ряд с меньшим знаменателем, например с
=1,26. Это ни в коем случае не означает, что знаменатель ряда передаточных отношений привода равен 1,26. Просто использован такой масштаб. Если для шкалы взять ряд с меньшим знаменателем, например с  =1,06, то на такой подробной шкале будет легче ориентироваться, но она займет гораздо больше места.
=1,06, то на такой подробной шкале будет легче ориентироваться, но она займет гораздо больше места.
При построении графика вначале отмечены точки, соответствующие частотам вращения вала электродвигателя, и определено общее минимальное передаточное отношение привода:
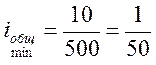
Эту величину следует разбить на 5 передаточных отношений, соблюдая требования к их предельно допустимым значениям. При этом надо проследить, чтобы в групповой передаче оба передаточных отношения также находились в допустимых пределах.

Передаточное отношение ременной передачи в данном примере принято: iр.п.= 1/1,281, так, чтобы на первом валу при максимальной частоте вращения электродвигателя получилась частота вращения 1600 об/мин. Такое решение чисто волевое, можно было выбрать и другое передаточное отношение.
Передаточное отношение i21 в групповой передаче назначено равным i21=1,26 (здесь тоже можно назначить и другую величину). В соответствии с величиной знаменателя ряда передаточных отношений коробки (выше показано, что  ) значение другого передаточного отношения группы будет:
) значение другого передаточного отношения группы будет:
 .
.
Передаточное отношение прямой передачи с вала I на вал V получено из уравнения кинематического баланса:
 . i4=1,24
. i4=1,24
Передаточные отношения двух одиночных передач назначены:
i2=1 и i3=1/4.
Тогда передаточное отношение i1 получается из общего минимального передаточного отношения:
 , т.е.
, т.е. 
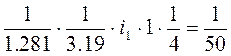 , откуда
, откуда  .
.
Теперь следует составить уравнения кинематического баланса для всех кинематических цепей, начиная уравнения с двух частот вращения двигателя 2050 и 500 об/мин, и рассчитать частоты вращения, получающиеся при этом на последнем валу. Отметив эти частоты, как показано на рис. 3.3, нужно проверить, осуществляется ли перекрытие частот вращения, и получаются ли максимальная и минимальная частота. Понятно, что частоты вращения, которые получаются в промежутке между максимальной и минимальной частотой вовсе не должны совпадать с какими-то стандартными частотами – ведь спроектирован бесступенчатый привод.
Определение чисел зубьев для групповой передачи в данном случае не удастся выполнять с помощью таблиц, приведенных в п. 2.11, поскольку передаточные отношения (или одно из них) не равны целой степени какого-либо стандартного знаменателя ряда. Придется воспользоваться методом наименьшего общего кратного, который описан в п. 2.11. Определение чисел зубьев в одиночных передачах, как обычно, выполняется методом подбора.
Когда определяется количество ступеней присоединяемой к двигателю коробки, то иногда приходится округлять это значение на значительную величину, например, Z=3,2 округлять до Z=4. В этом случае кроме небольшого перекрытия, обусловленного принятым коэффициентом запаса, на шкале частот вращения получается значительное перекрытие в области перехода от работы одной серии передач к другой. С этим приходится мириться.
Дата добавления: 2015-04-15; просмотров: 287; Мы поможем в написании вашей работы!; Нарушение авторских прав |