
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введем обозначения



Замечание: в механике, физике, а последнее десятилетие – в математике производные по времени обозначают точками. Тогда равенство (*) перепишем  (**)
(**)
Проинтегрируем (**) по времени, тем самым получим S(t)
 (5) – связь между координатным и естественным способами.
(5) – связь между координатным и естественным способами.
Замечание: (5) записано в предположении, что точка М начинает двигаться из начала отсчета О, т.е. S(0)=0, все время в положительном направлении. Для последнего, как покажем дальше, достаточно чтобы функция под интегралом (5) не обращалась в ноль на интервале (0;t)
Скорость и ускорение точки.
Основными кинематическими характеристиками движения точки является скорость и ускорение, это векторные величины.
Вектор скорости.
Пусть задан векторный способ. Если в момент t для положения М радиус-вектор  , а в последующий момент t1>t радиус-вектор стал
, а в последующий момент t1>t радиус-вектор стал  ,то вектором перемещения за время Δt=t1-t называется вектор
,то вектором перемещения за время Δt=t1-t называется вектор  .
.
 z
z














y
x
Из Δ ОММ1  , отсюда
, отсюда  , т.е. вектор перемещения представляет превращение радиус-вектора за время Δt.
, т.е. вектор перемещения представляет превращение радиус-вектора за время Δt.
Средней скоростью точки за время Δt называется отношение  (1)
(1)
Чем меньше интервал Δt, тем точнее вектор  описывает движение точки.
описывает движение точки.
Переходя в (1) к пределу при  , получим мгновенную скорость, т.е. скорость в момент t.
, получим мгновенную скорость, т.е. скорость в момент t. 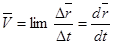 , т.е. скорость точки в данный момент есть производная радиус-вектора по времени
, т.е. скорость точки в данный момент есть производная радиус-вектора по времени  (2). Поскольку предельное направление хорды ММ1, когда дуга ММ1 стягивается к точке, есть направление касательной в этой точке. Вектор мгновенной скорости
(2). Поскольку предельное направление хорды ММ1, когда дуга ММ1 стягивается к точке, есть направление касательной в этой точке. Вектор мгновенной скорости  по касательной к траектории.
по касательной к траектории.
Ускорение точки.
Ускорение характеризует изменение вектора скорости во времени.
 M,t
M,t








Δ  М1,t
М1,t



Пусть в момент времени t в положении М скорость точки была V, а в последующий момент t1>t в положении М1 скорость стала V1. Тогда за время Δt=t1-t>0 скорость получает приращение 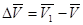 .
.
Построим вектор  . Для этого перенесем
. Для этого перенесем  параллельно в точку М и построим параллелограмм, где
параллельно в точку М и построим параллелограмм, где  - диагональ,
- диагональ,  - одна из сторон, тогда другая сторона даст вектор
- одна из сторон, тогда другая сторона даст вектор  . Можно доказать, что если дуга траектории ММ1достаточно мала, то вектор
. Можно доказать, что если дуга траектории ММ1достаточно мала, то вектор  будет направлен в сторону вогнутости траектории.
будет направлен в сторону вогнутости траектории.
Средним ускорением за время Δt будет отношение
 (*)
(*)
Среднее ускорение направлено в сторону  . Вектор
. Вектор  те точнее характеризует изменение скорости, чем меньше Δt. Перейдя поэтому в (*) к пределу при
те точнее характеризует изменение скорости, чем меньше Δt. Перейдя поэтому в (*) к пределу при  , получим мгновенное ускорение точки, т.е. ускорение в момент t.
, получим мгновенное ускорение точки, т.е. ускорение в момент t.

(1)
Вектор мгновенного ускорения, т.е. ускорения в данный момент, равен производной от вектора скорости точки, учитывая, что скорость в свою очередь равна  , то
, то  (2). Вектор
(2). Вектор  по сказанному раннее также направлен в сторону вогнутости траектории. Если траектория – плоская кривая, то
по сказанному раннее также направлен в сторону вогнутости траектории. Если траектория – плоская кривая, то  , как и все остальные векторы здесь, лежит в плоскости траектории. Если траектория прямолинейная, то возможны два случая:
, как и все остальные векторы здесь, лежит в плоскости траектории. Если траектория прямолинейная, то возможны два случая:


 а) М
а) М 

Это случай, когда величина скорости вырастает, т.е. движение ускоренное.
б)  М
М 



здесь скорость по величине убывает, т.е. движение замедленное.
Скорость и ускорение точки при
координатном способе задания движения.
Пусть задан координатный способ, т.е. прямоугольные координаты точки известны как функции времени. Запишем связь между векторным и координатным способами.
 (1)
(1)
Поскольку в (1) орты  ,
,  ,
,  - постоянные векторные множители, то для определения скорости точки будем дифференцировать (1) по времени, применяя обычные правили дифференцирования, т.е. вынося в каждом из слагаемых орты за знак производной.
- постоянные векторные множители, то для определения скорости точки будем дифференцировать (1) по времени, применяя обычные правили дифференцирования, т.е. вынося в каждом из слагаемых орты за знак производной.
 (2)
(2)
Если записать вектор  также через его проекции на оси
также через его проекции на оси  , то сравнивая это равенство с (2), находим
, то сравнивая это равенство с (2), находим  ,
,  ,
,  (3), т.е. проекциями скорости при координатном способе будут производные от соответствующих прямоугольных координат точки.
(3), т.е. проекциями скорости при координатном способе будут производные от соответствующих прямоугольных координат точки.
Величина скорости будет  (4), направление можно определить направляющими косинусами, т.е. косинусами углов между вектором скорости и осями координат:
(4), направление можно определить направляющими косинусами, т.е. косинусами углов между вектором скорости и осями координат:

 (5)
(5)
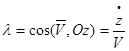
Как для направляющих косинусов справедливо тождество 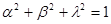 (6). Ход определения ускорения при координатном способе полностью аналогичен приведенным вычислениям для скорости. В частности при вычислении вектора ускорения следует дифференцировать равенство (2) для скорости, тогда, применяя те же правила дифференцирования, получим
(6). Ход определения ускорения при координатном способе полностью аналогичен приведенным вычислениям для скорости. В частности при вычислении вектора ускорения следует дифференцировать равенство (2) для скорости, тогда, применяя те же правила дифференцирования, получим
 (7)
(7)
т.е. сразу получаем проекции ускорения 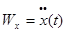 ,
,  ,
,  (8), они равны вторым производным от соответствующих координат.
(8), они равны вторым производным от соответствующих координат.
Величина ускорения так же будет
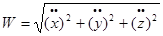 (9),
(9),
а направление, по аналогии со скоростью, определяют по направляющим косинусам:

 (10)
(10)

Для этих косинусов также справедливо тождество (6).
Формулы (2)-(10) полностью определяют векторы скорости и ускорения при координатном способе.
Скорость точки при естественном способе.



 _ O
_ O

 М,t,S
М,t,S



M1,t1,S1
О/ 
+
Пусть при естественном способе т. М в момент t имела криволинейную координату S, а в последующий момент t1 в положении М1 эта координата стала S1, значит за время Δt=t1-t>0 криволинейная координата изменяется на ΔS=S1-S. Для простоты считаем, что ΔS>0, т.е. точка движется в положительном направлении. Введем также векторный способ задания движения, т.е. т. О/ начала отсчета радиус-вектора  движущейся материальной точки. Запишем вектор скорости точки М через предел
движущейся материальной точки. Запишем вектор скорости точки М через предел
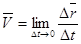
Величина скорости тогда будет:  (*).
(*).
При вычислении придела (*) величина вектора перемещения, т.е.  близка к соответствующей длине дуги, т.е. ΔS. Это эквивалентная бесконечно малая (если траектория – гладкая кривая), т.е.
близка к соответствующей длине дуги, т.е. ΔS. Это эквивалентная бесконечно малая (если траектория – гладкая кривая), т.е.  , при
, при  ,
,  .
.
Поэтому в пределе (*) величину  заменим на эквивалентную, т.е. ΔS, тогда
заменим на эквивалентную, т.е. ΔS, тогда  или
или  (1), т.е. скорость по величине есть производная от криволинейной координаты по времени.
(1), т.е. скорость по величине есть производная от криволинейной координаты по времени.
Замечание: равенство (1) записано в предположении, что координата S возрастает, т.е. что  . В общем случае аналогично доказывается, что величина скорости будет
. В общем случае аналогично доказывается, что величина скорости будет  (2).
(2).
Для записи вектора скорости при естественном способе вводят орт  касательной к траектории, направленный в сторону скорости, тогда
касательной к траектории, направленный в сторону скорости, тогда  записывается просто:
записывается просто:  (3), где величина V определяется формулами (1) или (2).
(3), где величина V определяется формулами (1) или (2).
Ускорение точки при естественном способе.
Касательное и нормальное ускорения.
1. Кривизна и радиус кривизны плоской кривой.
При вычислении ускорения для естественного способа будем рассматривать частный случай плоской траектории точки. Все выводы и формулы для этого случая справедливы и в общем случае пространственного движения.
Покажем орты касательных к траектории для двух соседних положений точки на ней М и М1.


 М1
М1




ε 
М
Перенесем орт  параллельно в точку М. Угол между ортами ε называется углом смежности. Средней кривизной плоской кривой называют отношение угла смежности к соответствующей длине дуги, т.е.
параллельно в точку М. Угол между ортами ε называется углом смежности. Средней кривизной плоской кривой называют отношение угла смежности к соответствующей длине дуги, т.е.  (*).
(*).
В пределе здесь, когда длина дуги  , т.е.
, т.е. 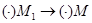 , получим точное значение кривизны, т.е. кривизну кривой в точке М:
, получим точное значение кривизны, т.е. кривизну кривой в точке М:
 (1)
(1)
Величина, обратная К, называется радиусом кривизны  плоской крывой, т.е.
плоской крывой, т.е.  (2); [K]=1/м ,
(2); [K]=1/м ,  м.
м.
Вычислим радиус кривизны для двух простых случаев:
А) траектория – окружность
Для окружности угол смежности ε равен соответствующему центральному углу φ, это углы со взаимно перпендикулярными сторонами, поэтому

 ,
,  , т.е. для окружности радиус кривизны совпадает с ее радиусом R.
, т.е. для окружности радиус кривизны совпадает с ее радиусом R.
M 

 |





 R φ ε
R φ ε

 M1
M1

В) траектория – прямолинейная
М  M1
M1 

ε=0, К=0, Кср=0, 
Т.е. для прямолинейного участка траектории радиус кривизны бесконечен.
2. Производная орта касательной по криволинейной координате.
 |


M1



 a b
a b

M 

При движении точки по траектории орт касательной  будет функцией криволинейной координаты ρ, поэтому имеет смысл производная
будет функцией криволинейной координаты ρ, поэтому имеет смысл производная  , найдем ее.
, найдем ее.
Рассмотрим равнобедренный треугольник Мab, образованный ортами  ,
,  . Из него следует, что
. Из него следует, что  ,
,  . Т.е. вектор
. Т.е. вектор  есть приращение орта
есть приращение орта  на дуге
на дуге  . По величине он равен:
. По величине он равен:  это следует из Δмab. Вычислим
это следует из Δмab. Вычислим  (*) по модулю:
(*) по модулю:
 ,
,
доказали, что  (1).
(1).
Кроме орта  , вводим также орт внутренней нормали
, вводим также орт внутренней нормали  к траектории. Заметим, что при вычислении производной (*) как предела, т.е.
к траектории. Заметим, что при вычислении производной (*) как предела, т.е.  , вектор
, вектор  в пределе будет направлен именно вдоль орта
в пределе будет направлен именно вдоль орта  . Поскольку в Δмab при
. Поскольку в Δмab при  ,
,  . Тем самым доказали равенство, что
. Тем самым доказали равенство, что 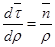 (2) (одна из формул Бине).
(2) (одна из формул Бине).
3.  Разложение вектора ускорения на касательное и нормальное.
Разложение вектора ускорения на касательное и нормальное.






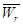


М 



Разложим  графически на две ортогональные составляющие: касательное и нормальное ускорения
графически на две ортогональные составляющие: касательное и нормальное ускорения  =
= 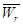 +
+  (3). Для определения величин Wτ и Wn следует дифференцировать по времени вектор скорости при естественном способе.
(3). Для определения величин Wτ и Wn следует дифференцировать по времени вектор скорости при естественном способе.
 Здесь оба множителя зависят от t, поэтому используем формулу дифференцирования произведения
Здесь оба множителя зависят от t, поэтому используем формулу дифференцирования произведения  (**) Здесь во втором слагаемом производную
(**) Здесь во втором слагаемом производную  преобразуем с помощью формулы (2)
преобразуем с помощью формулы (2)

Тогда (**) дает  (4). Тем самым нашли векторы касательного и нормального ускорения в (3)
(4). Тем самым нашли векторы касательного и нормального ускорения в (3)
 ,
,  (5)
(5)
Часто в кинематике под нормальным и касательным ускорениями понимают проекции этих векторов на соответствующие орты, т.е.  ,
,  (6). Т.е. касательное ускорение есть производная от величины скорости, а нормальное равно квадрату скорости деленному на радиус кривизны.
(6). Т.е. касательное ускорение есть производная от величины скорости, а нормальное равно квадрату скорости деленному на радиус кривизны.
Из (5) и (6) видно, что вектор  может иметь либо направление
может иметь либо направление  , т.е. скорости, когда
, т.е. скорости, когда  (движение ускоренное), либо противоположное направление, когда
(движение ускоренное), либо противоположное направление, когда 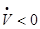 (движение замедленное).
(движение замедленное).
Частные случаи движения точки.
1. Равномерное движение. Это движение, при котором скорость точки постоянна по величине, V=const.
Замечание: траектория точки при этом может быть криволинейной. При этом  ,
,  - начальная криволинейная координата.
- начальная криволинейная координата.  , т.е. при равномерном движении полное ускорение состоит только из нормального
, т.е. при равномерном движении полное ускорение состоит только из нормального  .
.
2. Прямолинейное движение (не обязательно равномерное).
Для прямолинейной траектории радиус кривизны  , тогда
, тогда  , т.е. в этом случае полное ускорение, наоборот, состоит из касательного
, т.е. в этом случае полное ускорение, наоборот, состоит из касательного 
3. Равномерное движение – движение с постоянным по величине и знаку касательным ускорением,  . Обычно этот случай разделяют на два: равноускоренное движение, когда
. Обычно этот случай разделяют на два: равноускоренное движение, когда  , и равнозамедленное
, и равнозамедленное 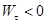 . В обоих случаях справедливы равенства:
. В обоих случаях справедливы равенства:

 V0 – начальная скорость
V0 – начальная скорость

 - начальная координата, обычно полагается =0, т.е. при равнопеременном движении скорость изменяется по линейному закону, а криволинейная координата
- начальная координата, обычно полагается =0, т.е. при равнопеременном движении скорость изменяется по линейному закону, а криволинейная координата  по квадратичному во времени.
по квадратичному во времени.
Простейшие движения твердого тела
К простейшим в кинематике относят два типа движений: поступательное движение и вращение вокруг неподвижной оси.
1. Поступательное движение – движение, при котором любая прямая, проведенная в нем, остается параллельна самой себе.
Примеры: движение кузова автомобиля на прямолинейной дороге (в этом случае траектории всех точек кузова – это параллельные прямые); круговое поступательное движение:


 С
С
 А В АВ - спарник
А В АВ - спарник




 О О1
О О1





Если длины кривошипов равны ОА=О1В, то спарник АВ совершает поступательное круговое движение, т.е. все его точки движутся по окружностям одинаковых радиусов, но со сдвинутыми центрами.
Вообще траекториями точек тела при поступательном движении могут быть любые кривые.
Справедлива теорема: при поступательном движении тела траектории всех его точек равны, т.е. при наложении совпадают, а скорости и ускорения векторно равны.












 Z B/
Z B/
 A/
A/

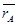 1 2
1 2
y
x
Выделим в теле, движущемся поступательно, отрезок АВ. Поскольку при движении он сохраняет параллельность, а величина его также неизменна (как расстояние между точками твердого тела), то  . Последнее означает, что траектория точки В получается из траектории точки А ее параллельным переносом на вектор
. Последнее означает, что траектория точки В получается из траектории точки А ее параллельным переносом на вектор  , т.е. траектории действительно равны, т.к. при наложении совпадут.
, т.е. траектории действительно равны, т.к. при наложении совпадут.
Рассмотрим векторный треугольник ОАВ. Из него видно, что 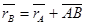 . Будем дифференцировать это равенство по времени
. Будем дифференцировать это равенство по времени
 , т.е.
, т.е.  . Доказали равенство скоростей. Дифференцируя его также по времени, подучим и равенство ускорений точек
. Доказали равенство скоростей. Дифференцируя его также по времени, подучим и равенство ускорений точек  .
.
Следствие: из доказанной теоремы видно, что все точки тела при поступательном движении движутся одинаково, поэтому при поступательном движении можно говорить о скорости, ускорении и траектории такого движения, приписывая их к любой точки тела.
2. Вращательное движение.





 Рассмотрим простейшее вращательное движение, когда тело вращается вокруг неподвижной оси Z.
Рассмотрим простейшее вращательное движение, когда тело вращается вокруг неподвижной оси Z.

 Z
Z
М0 О
М
При таком вращении точки тела, лежащие на оси, остаются неподвижными, а любая точка М, отстающая от оси на расстоянии ОМ=h, будет совершать движение по окружности радиуса h с центром на оси. Плоскости таких окружностей перпендикулярны оси.
Для того, чтобы задать вращательное движение достаточно для любой точки М тела, не лежащей на оси задать угол  , где М0 – положение этой точки в начальный момент времени t0=0. Угол φ в радианах называется угловой координатой тела, а уравнение
, где М0 – положение этой точки в начальный момент времени t0=0. Угол φ в радианах называется угловой координатой тела, а уравнение  (1) называется уравнением или законом вращения. Положительное направление отсчета φ принимают против часовой стрелки, если смотреть с положительного направления оси Z. Основными кинематическими характеристиками вращательного движения являются его угловая скорость и угловое ускорение тела.
(1) называется уравнением или законом вращения. Положительное направление отсчета φ принимают против часовой стрелки, если смотреть с положительного направления оси Z. Основными кинематическими характеристиками вращательного движения являются его угловая скорость и угловое ускорение тела.
Угловая скорость определяет изменение угла φ во времени. Пусть в момент t угловая координата была φ, а в последующий момент t1>t она стала φ1, т.е. за время Δt= t1-t угловая координата получает приращение Δφ=φ1-φ, тогда средней угловой скоростью за время Δt называется величина  (2).
(2).  тем точнее характеризует изменение угла φ, чем меньше Δt , поэтому, перейдя здесь к пределу при
тем точнее характеризует изменение угла φ, чем меньше Δt , поэтому, перейдя здесь к пределу при  , получим точное значение угловой скорости в момент t
, получим точное значение угловой скорости в момент t
 или
или  (3)
(3)
Таким образом, мгновенная угловая скорость – есть производная угловой координаты по времени. Заметим, что 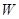 может быть разных знаков в зависимости от того, в какую сторону вращается тело: при положительном направлении вращения
может быть разных знаков в зависимости от того, в какую сторону вращается тело: при положительном направлении вращения 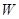 >0, т.к.
>0, т.к.  возрастает.
возрастает.
[W]=рад/с=с-1
В технике часто для измерения угловых скоростей многооборотных вращений (турбин, валов и т.д.) применяют внесистемную единицу измерения угловых скоростей [n]=об/мин

Угловое ускорение характеризует изменение угловой скорости во времени, так, если за тот же промежуток времени Δt угловая скорость изменялась от W до W1, т.е. получила приращение ΔW=W1-W, то угловое ускорение будет
 (4)
(4)
Переходя в (4) к пределу, получим мгновенное угловое ускорение, т.е. ускорение в момент t: 
 (5), т.е. угловое ускорение в данный момент есть производная от угловой скорости. Учитывая определение W , получим
(5), т.е. угловое ускорение в данный момент есть производная от угловой скорости. Учитывая определение W , получим  (6), т.е. это также вторая производная от угловой координаты [ε]=рад/с2=с-2 . Вращение будет ускоренным (т.е. величина W возрастает), если W и ε одинаковых знаков, и замедленным, если они разных знаков.
(6), т.е. это также вторая производная от угловой координаты [ε]=рад/с2=с-2 . Вращение будет ускоренным (т.е. величина W возрастает), если W и ε одинаковых знаков, и замедленным, если они разных знаков.
В кинематике часто используют векторные представления угловой скорости и углового ускорения, т.е. считают, что  (7), где
(7), где  - орт оси Z. Причем вектор
- орт оси Z. Причем вектор  отсчитывают от любой точки на оси. Угловое ускорение считают также вектором
отсчитывают от любой точки на оси. Угловое ускорение считают также вектором  (8). Из (7) и (8) видно, что векторы W и ε связаны равенством (5), т.е.
(8). Из (7) и (8) видно, что векторы W и ε связаны равенством (5), т.е.  (9). Вектор
(9). Вектор  направлен в сторону
направлен в сторону  , если вращение ускоренное, и в противоположную сторону, если замедленное. Величины W и ε разных знаков.
, если вращение ускоренное, и в противоположную сторону, если замедленное. Величины W и ε разных знаков.


 В
В









 z
z



А
 Линейные скорость и ускорение точек вращающегося тела.
Линейные скорость и ускорение точек вращающегося тела.
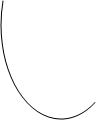
Покажем, что, зная величины угловой скорости W и условия ускорения E, можно легко найти и векторы скорости и ускорений в любой точке вращающегося тела, отстоящей на расстоянии h от оси. 



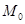 О
О








 М
М 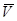

Поскольку траектория точки М во вращательном движении известно - это дуга окружности радиуса ОМ=h, для то определения скорости и ускорений удобно использовать естественная способ задания движения, принимая в качестве криволинейной координаты длину дуги окружности ММ 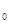 .
.
 Тогда:
Тогда:  =
= 

 (1)
(1)
Таким образом, величина скорости ваг вращательном движении есть произведение расстояния h на угловую скорость тела.
Вектор  точки М направлен по касательной к окружности радиуса ОМ, т.е. ортогонально этому радиусу. Отсюда следует эпюра скоростей точек вращающегося тела, лежащих на одном радиусе.
точки М направлен по касательной к окружности радиуса ОМ, т.е. ортогонально этому радиусу. Отсюда следует эпюра скоростей точек вращающегося тела, лежащих на одном радиусе.

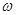 М
М












 о
о
Касательное ускорение по величине будет: 
 (2)
(2)
Касательное ускорение равно произведению расстояния h на угловое ускорение тела.
Замечание: в формуле (2) E может быть как больше, так и меньше нуля.
В первом случае вектор  направлен в сторону скорости, во втором – в противоположную. Для определения величины нормального ускорения так же применим общую формулу нормального ускорения из кинематики точки:
направлен в сторону скорости, во втором – в противоположную. Для определения величины нормального ускорения так же применим общую формулу нормального ускорения из кинематики точки:


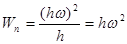 (3)
(3)
Таким образом, нормальное ускорение по величине не есть произведение расстояния h на квадрат угловой скорости.
Полное ускорение будет тогда:

 (4)
(4)
Из формул 1-4 видно, что, зная 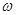 и E, можно полностью определить векторы
и E, можно полностью определить векторы 
Замечание: поскольку  и
и  также пропорциональны h, то получаем аналогичное правило для определения эпюры ускорений.
также пропорциональны h, то получаем аналогичное правило для определения эпюры ускорений.



 M
M



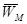

 E
E


 O
O



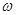
Все векторы ускорений точек на радиусе OM параллельны  , т.е. ускорению точек на ободе диска.
, т.е. ускорению точек на ободе диска.
Дата добавления: 2015-04-15; просмотров: 323; Мы поможем в написании вашей работы!; Нарушение авторских прав |