Сложное движение точки.

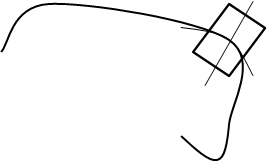
Сложное или составное движение – это движение точки по отношению к двум системам отсчета, одна из них, связанная с неподвижным толом “B” называется абсолютной, а другая – подвижная система “A” движется относительно неподвижной “B”.

z

r

A a

M

e

y

x B

Точка М перемещается внутри или по поверхности тела А, которое еще называется переносной средой (поскольку оно не всегда обязательно твердое). В свою очередь тело А перемещается относительно условно неподвижного тела В.

Пример: движение куска руды относительно конвейера, который перемещается вдоль выработки.

Движение точки М относительно подвижного тела А называется относительным, траектория, скорость такого движения также будут относительными траектории, скорости и ускорения. Относительное движение увидит наблюдатель находящийся вместе с телом А.

На рисунке можем изобразить лишь какой-то фрагмент относительной траектории, поскольку она перемещается вместе с телом А.

Движение точки М вместе с телом А относительно неподвижного тела В, называется переносным движением. Точнее, переносное это движение той точки переносной среды А, относительно неподвижного тела В с которым в данный момент совпадает точка М. Траектория, скорость и ускорение этого движения также соответственно будут переносными траектории скоростью и ускорения.

Движение точки М по отношению к неподвижному телу В или к неподвижной системе отсчета называется абсолютным или составным движением. Именно абсолютное движение видит наблюдатель связанный неподвижным телом В. Траектория, скорость и ускорение - абсолютные траектория, скорость и ускорение.

Пример: движение ползуна вдоль вращающегося кривошипа.

3 2

А

О

Движение ползуна вдоль кривошипа ОА относительное. Фрагментами относительных траекторий будут фрагменты кривых вдоль кривошипа до соответствующих положений ползуна. Переносным движением будет вращательное движение точки К кривошипа, через которые в данный момент проходит ползун. Поэтому фрагментами переносных траекторий будут фрагменты окружностей соответствующего радиуса ОР.

Составным или абсолютным движением будет движение ползуна относительно неподвижного основания, его траекторию получим, соединяя различные положения ползуна Р. В данном случае абсолютная траектория это некоторая разворачивающаяся спираль.