
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частные случаи вращательного движения.
1) Равномерное вращение – вращение с постоянной угловой скоростью.

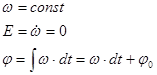
При равномерном вращении угол поворота 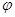 линейно возрастает во времени.
линейно возрастает во времени.
2)Равнопеременное вращение – вращение с постоянным угловым ускорением. Так же как и в случае равнопеременного движения точки здесь выделяют равноускоренное вращение (E>0) и равнозамедленное (E<0)
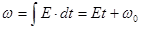
 здесь:
здесь: 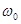 - начальная угл. скорость
- начальная угл. скорость

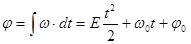
т.е. формулы для 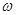 и
и 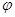 здесь полностью аналогичны формулам для величины скорости и криволин. координаты S при равнопеременном движении точки.
здесь полностью аналогичны формулам для величины скорости и криволин. координаты S при равнопеременном движении точки.



















 В частном случае равноускоренного вращения при нулевой начальной скорости можно получить простую формулу для полного угла поворота, зная конечную угловую скорость.
В частном случае равноускоренного вращения при нулевой начальной скорости можно получить простую формулу для полного угла поворота, зная конечную угловую скорость.
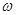

здесь  - конечная угловая
- конечная угловая
 скорость, соотв. моменту
скорость, соотв. моменту 
0 

Пример:





 R
R




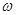 o
o 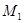

 |
Дано:

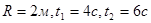
Найти:
 (полное число оборотов)
(полное число оборотов)
Решение:
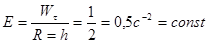
(случай равноускор. Вращения)

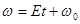


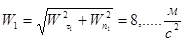
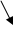

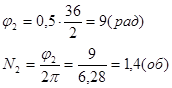
Векторные формулы скорости и ускорения точек вращающегося тела.
Будем определять вектор  точки
точки  вращающегося тела, угловая скорость которого
вращающегося тела, угловая скорость которого 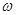 , отсчитывается от произвольной точки,
, отсчитывается от произвольной точки, 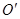 но оси. Вектор
но оси. Вектор 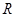 точки,
точки, 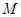 отсчитываемый от того же начала
отсчитываемый от того же начала 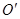 . Покажем, что для скорости точки
. Покажем, что для скорости точки  справедливо векторное равенство:
справедливо векторное равенство:
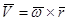 (1)
(1)





 z
z



 B
B
 | |||
 |

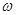

 o
o
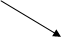
 M
M














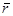

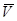
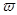
 A
A
По определению векторного приведения величина его здесь будет 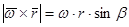 (*) . Здесь, как следует из
(*) . Здесь, как следует из 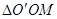

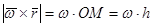 получим обычную скалярную скорость во вращательном движении. Тем самым доказали равенство (1) по величине. По направлению векторное произведение (1) должно быть направлено перпендикулярно плоскости
получим обычную скалярную скорость во вращательном движении. Тем самым доказали равенство (1) по величине. По направлению векторное произведение (1) должно быть направлено перпендикулярно плоскости 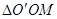 в ту сторону, откуда поворот вектора
в ту сторону, откуда поворот вектора 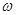 к вектору
к вектору 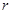 на наименьший угол виден против часовой стрелки. Все то же самое можно сказать и о направлении вектора
на наименьший угол виден против часовой стрелки. Все то же самое можно сказать и о направлении вектора 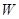 . Таким образом, равенство (1) обосновали и по направлению. Для полного ускорения
. Таким образом, равенство (1) обосновали и по направлению. Для полного ускорения  точки
точки 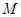 продифференцируем (1) по времени используя правило дифференцирования векторных произведений:
продифференцируем (1) по времени используя правило дифференцирования векторных произведений:


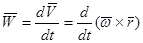

E 
В результате приходим к равенству: 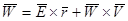 (2) это формула Ривальса.
(2) это формула Ривальса.
Можно доказать, что первое векторное произведение здесь представляет касательное ускорение точки, а второе нормальное ускорение:
 |
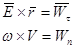 (3)
(3)
Дата добавления: 2015-04-15; просмотров: 1250; Мы поможем в написании вашей работы!; Нарушение авторских прав |