
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема сложения скоростей и ускорений в составном движении.
1) Теорема сложения скоростей.
При составном движении точки её абсолютная скорость складывается из векторов относительной и переносной скоростей.
 (1)
(1)
примеры: найдем абсолютную скорость в предыдущем примере.
 А
А

 |







 Р
Р


 |












 О
О

 Движение ползуна началось из центра “O”.
Движение ползуна началось из центра “O”.
Поскольку переносное движение, здесь вращательное с радиусом ОР то переносная скорость  направлена, перпендикулярна этому радиусу. Так как здесь векторы
направлена, перпендикулярна этому радиусу. Так как здесь векторы  и
и  ортогональны их сумма, то есть относительная скорость определяется по теореме Пифагора:
ортогональны их сумма, то есть относительная скорость определяется по теореме Пифагора:
 , здесь,
, здесь,  следовательно
следовательно 
Вообще с помощью теоремы (1) построив соответствующий параллелограмм скоростей можно всегда найти какую либо одну скорость по двум другим.
2)Теорема сложения ускорений.
Рассмотрим два случая: упрощенный и усложненный
Упрощенный (когда переносное движение поступательное)
Дифференцируя (1) по времени здесь легко получить  (2) т.е. здесь также абсолютное ускорение векторно складывается из относительного и переносного. Следовательно, также должен выполнятся параллелограм ускорений:
(2) т.е. здесь также абсолютное ускорение векторно складывается из относительного и переносного. Следовательно, также должен выполнятся параллелограм ускорений:








Как и в предыдущем примере зная, например один из векторов ускорений здесь и один из углов (любой) в параллелограмме, можно найти два других вектора.
2. Усложненный случай (случай вращательного переносного движения).
Здесь вводят вектор угловой скорости переносного вращения. Тогда теорема сложения ускорений записывается так:
 (3)
(3)
т.е. здесь появляется дополнительное ускорение  - ускорение Кориолиса, для него справедливо векторное равенство:
- ускорение Кориолиса, для него справедливо векторное равенство:
 (4)
(4)
Если в (4) положить,  то видно, что
то видно, что  обратится в ноль, то получается предыдущий случай пост. Переносного движения.
обратится в ноль, то получается предыдущий случай пост. Переносного движения.










 Пример: С
Пример: С 



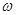


М


О
Ю
Построим для точки М ускорение в ф.(3). Здесь вектор ускорения  по правилу векторного произведения будет направлен вдоль соответствующей параллели на восток. Возникает закон БЭРа: такое ускорение Кориолиса приводит к тому, что в частицы воды в реках текущих с севера на юг имеют некоторое восточное ускорение, по законам динамики, они с соответствующей силой “давят” на западный берег, т.е. подмывают его.
по правилу векторного произведения будет направлен вдоль соответствующей параллели на восток. Возникает закон БЭРа: такое ускорение Кориолиса приводит к тому, что в частицы воды в реках текущих с севера на юг имеют некоторое восточное ускорение, по законам динамики, они с соответствующей силой “давят” на западный берег, т.е. подмывают его.
Плоско-параллельное движение твердого тела и его свойства
Движение твердого тела называют плоскопараллельным (плоским) если любая точка тела во время движения остаётся на одном и том же расстоянии до некоторой неподвижной плоскости “P”.


 М Q
М Q









 S
S 




 P
P
В соответствии с этим определяем расстояние как от произвольной точки М тела до плоскости Р, так и от любой точки сечения S тела параллельного Р и проходящего через точку М, останется при движении одинаковым.
Последнее означает, что такое сечение S будет скользить в своей плоскости Q параллельно P.
Такое движение совершают многие части механизмов и машин. Например: движение кривошипно -шатунного механизма; качение кругового диска или цилиндра по ровному прямолинейному пути. Это частные случаи плоского движения. Вращение вокруг неподвижной оси рассмотренное ранее, так же частный случай таких движений. Таким образом, чтобы задать плоское движение, достаточно задать движение любого сечения S твердого тела в его плоскости.
Рассмотрим поэтому движение произвольной фигуры S, в её плоскости OXY, такое движение можно задавать, выбрав в этом сечении любой отрезок АВ и задавая движение этого отрезка. Последнее же легко задать, задавая движение конца А отрезка, его прямоугольными координатами и угол  , который отрезок составляет с осью OX. Следовательно, уравнениями плоскопараллельного движения будут следующие три:
, который отрезок составляет с осью OX. Следовательно, уравнениями плоскопараллельного движения будут следующие три:









 (1)
(1) 
s A 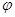 B
B



В общем случае движение твердого тела известно, что оно определяется шестью координатами (прямоугольными координатами, любой точки тела в пространстве и тремя углами поворота тела вокруг осей проходящих через эту точку). Такой способ задания плоского движения называют методом Полюса, а точку А, выбранную на S, полюсом.
Таким образом, уравнения (1) описывают поступательное движение фигуры S, вместе с плюсом (первые два уравнения) и вращение ее вокруг полюса. Очевидно, что первые два зависят от выбора полюса, однако угол поворота тела  , т.е. вращательная часть движения от выбора полюса не зависит. Последняя есть теорема Эйлера о независимости вращательного движения вокруг полюса.
, т.е. вращательная часть движения от выбора полюса не зависит. Последняя есть теорема Эйлера о независимости вращательного движения вокруг полюса.
Скорости точек при плоском движении. Определение их методом полюса.














S  M
M


 A
A 
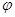




Будем определять скорость любой точки М фигуры S движущейся в плоскости OXY, выберем на S произвольный полюс A и свяжем с ним оси  параллельные соответственно OX и OYO. Также оси называют полу подвижными.
параллельные соответственно OX и OYO. Также оси называют полу подвижными.
Движение фигуры S по отношению к таким полу подвижным осям будет представляться, как вращение вокруг неподвижного центра А. построим радиус векторы  в точке М относительно О;
в точке М относительно О;  - ее вектор относительна полюса и
- ее вектор относительна полюса и  - вектор полюса относительно неподвижных осей.
- вектор полюса относительно неподвижных осей.
 (2)
(2)
Чтобы определить скорость точки М следует дифференцировать (2) по времени.
 (*)
(*)
здесь  - скорость тоске М в неподвижных осях.
- скорость тоске М в неподвижных осях.
 - скорость полюса в тех же осях.
- скорость полюса в тех же осях.
 - вращательная скорость точки М, вокруг полюса А.
- вращательная скорость точки М, вокруг полюса А.
 (3)
(3)
т.е. любой точке фигуры S складывается из скорости полюса и скорости этой точки во вращательном движении вокруг полюса.
Для определения последней следует знать угловую скорость фигуры S. Заметим, что согласно теореме Эйлера омега также не зависит от выбора полюса. 
Тогда в соответствии с кинематикой обычно вращательного движения имеем, что  (4)
(4)
 перпендикулярно
перпендикулярно  АМ.
АМ.










 Равенству (3) соответствует параллелограмм скоростей:
Равенству (3) соответствует параллелограмм скоростей:



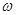
А 
 Спроектируем равенство (3) на направление отрезка АМ
Спроектируем равенство (3) на направление отрезка АМ
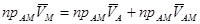 (5)
(5)
Получим тем самым теорему о равенстве проекций скоростей концов отрезка на его направление.
Мгновенный центр скоростей (МЦС).
Определение скоростей точек при плоском движении методом МЦС.
 Мгновенный центр скоростей (точки P) – это такая точка на плоской фигуре S или его мысленно продолженная скорость, которого равна нулю.
Мгновенный центр скоростей (точки P) – это такая точка на плоской фигуре S или его мысленно продолженная скорость, которого равна нулю.
Т.е. 











 Пусть известна скорость любого полюса А
Пусть известна скорость любого полюса А  и угловая скорость
и угловая скорость 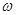 построим МЦС.
построим МЦС.
А 
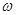
М

Р 
Для этого построим отрезок АР, причем АР перпендик.  и
и  . Определим скорости точки Р по методу полюса, т.е. (3) и (4):
. Определим скорости точки Р по методу полюса, т.е. (3) и (4):  (*)
(*)
Причем в (*) величина  , т.е. согласно (*)
, т.е. согласно (*)  . Зная теперь МЦС, скорость любой точки М согласно (3) найдем как вращательную скорость этой точки вокруг МЦС. Т.е.
. Зная теперь МЦС, скорость любой точки М согласно (3) найдем как вращательную скорость этой точки вокруг МЦС. Т.е.
 (6)
(6)
согласно (6) величина и направление скорости любой точки М будут:
 (7)
(7)




 MP
MP
таким образом, можно считать, что фигура S вращается в данный момент вокруг МЦС, однако в отличие от обычного вращательного движения здесь МЦС при движении изменяет свое положение.
Рассмотрим графические случаи определения МЦС.
1) скорости двух точек плоской фигуры не параллельны






 А
А
В
 |
Р 
2) скорости двух точек параллельны и не равны
 |
А


В 
Р







 2а)
2а) 
А
Р
 B
B








 3) Скорости двух точек параллельны и равны.
3) Скорости двух точек параллельны и равны.
А 
В 
М 
Здесь МЦС уходит в бесконечность, поэтому в соответствии с (7)  . Это случай мгновенного постоянного движения, для него скорость любой точки М:
. Это случай мгновенного постоянного движения, для него скорость любой точки М:













4) Качение без проскальзования.
 Качение без проскальзования по неподвижному основанию означает, что точка контакта тела с основанием - неподвижна. Т.е. это и будет МЦС.
Качение без проскальзования по неподвижному основанию означает, что точка контакта тела с основанием - неподвижна. Т.е. это и будет МЦС.
Р










































 Пример:
Пример:







a 

Определение скоростей точек 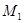 ……
…… 





Дата добавления: 2015-04-15; просмотров: 378; Мы поможем в написании вашей работы!; Нарушение авторских прав |