Относительное движение. Движение со связями.

5.1. Рыбак переправляется через реку, выдерживая курс перпендикулярно берегу. На какое расстояние снесет лодку, если ширина реки 100 м, а скорость лодки относительно воды вдвое больше скорости течения реки? [50 м]

5.2. Рыбак переправляется через реку шириной 100 м. Скорость лодки относительно воды вдвое меньше скорости течения. На какое минимальное расстояние относительно берега может снести лодку? Какое расстояние при этом пройдет лодка? [176 м; 200 м]

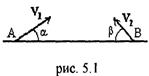
5.3. Корабль выходит из пункта A под углом a к линии берега. Одновременно из пункта B выпускают торпеду (рис 5.1). Под каким углом к берегу необходимо направить торпеду, чтобы она поразила корабль? Скорость корабля v₁ скорость торпеды v₂. [ ]

5.4. Человек находиться на расстоянии S от прямой дороги, по которой едет автобус со скоростью v. В тот момент, когда человек заметил автобус, расстояние между ними было равно L. С какой наименьшей скоростью должен бежать человек, чтобы успеть встретиться с автобусом? [ ]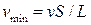

5.5. Поезд движется в восточном направлении со скоростью 27 км/ч и пассажиру кажется, что ветер дует с севера. Сохраняя прежнее направление движения, поезд увеличил скорость до 54 км/ч и пассажиру уже кажется, что ветер дует с северо-востока. Определить направление ветра и его скорость. [ветер дует с северо-запада со скоростью » 10,6 м/с]

5.6. Два корабля плывут навстречу друг другу со скоростями v₁ и v₂. В момент когда расстояние между ними равно L, с одного из кораблей взлетает голубь и летит к другому кораблю. Долетев до него, голубь разворачивается и летит обратно. Вернувшись к первому кораблю, голубь опять разворачивается и летит ко второму и т. д. Какое расстояние пролетит голубь до момента встречи кораблей, если он летает со скоростью v? [ ]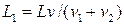

5.7. По двум прямым дорогам, угол между которыми равен 60 , удаляясь от перекрестка, движутся два автомобиля со скоростями 10 м/с и 20 м/с. В момент t = 0 расстояние между автомобилями равно 300 м. Через какое время расстояние между ними удвоится? [ ]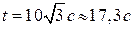

5.8. Две частицы движутся со скоростями v₁ и v₂ по двум взаимно перпендикулярным прямым к точке их пересечения. В момент t = 0 частицы находились на расстояниях L₁ и L₂ от перекрестка. Через какое время расстояние между частицами будет минимальным? [ ]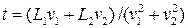

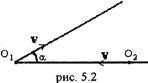
5.9. Два тела равномернодвижутся по прямым, пересекающимся под углом a (рис. 5.2). Скорости тел одинаковы и равны v. В момент t = 0 тела находились в точках O₁ и O₂. Расстояние O₁O₂ = L. Через какое время расстояние между телами будет наименьшим и каково это расстояние? [ ]

5.10. Теплоход движется по озеру параллельно берегу со скоростью v₁ = 25 км/ч. От берега отходит катер со скоростью v₂ = 40 км/ч. Через какое наименьшее время катер сможет догнать теплоход, если в начальный момент теплоход и катер находились на одной нормали к берегу и расстояние между ними было S = 1 км? [0,032 ч]

5.11. Мальчик ростом 1,5 м бежит со скоростью 3 м/с под фонарем, который висит на высоте 3 м. Скакой скоростью перемещается тень от головы мальчика? [6 м/с]

5.12. Луч света падает на экран ОА, который вращается вокруг оси O (рис. 5.3). Луч образует на экране зайчик С. Угловая скорость вращения экрана w, угол между лучом и горизонтом a. С какой скоростью перемещается зайчик по экрану, когда экран проходит вертикальное положение? Расстояние OC в этот момент равно l. [ ]

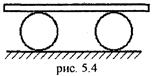
5.13. Платформа перемещается на двух круглых одинаковых катках (рис. 5.4). На сколько передвинулся каждый каток, если платформа передвинулась на 10 см? [5 см]

5.14. Доска длиной l одним концом лежит на цилиндре, а другой конец удерживается человеком (рис. 5.5). Человек начинает толкать доску вперед, вследствие чего цилиндр катится без проскальзывания. Какой путь должен пройти человек, чтобы дойти до цилиндра? [2l]

5.15. Снаряд, летящий горизонтально со скоростью v, разрывается на большое число осколков, разлетающихся во все стороны с одинаковыми скоростями. Найти скорость осколков, летящих вертикально относительно земли, если максимальная скорость осколков равна u. [ ]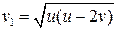

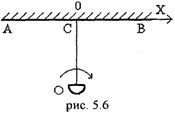
5.16. Прожектор O установлен на расстоянии l = 100 м от стены AB и бросает светлое пятно на стену (рис. 5.6). Прожектор вращается, делая один оборот за Т = 20 с. Написать уравнение движения x(t) светлого пятна по стене. За начало отсчета принять момент, когда пятно находится в точке C.

[ ]

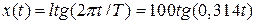5.17. Три черепахи находятся в вершинах равностороннего треугольника со стороной a. Они начинают одновременно двигаться с постоянными по модулю скоростями v, причем первая черепаха все время держит курс на вторую, вторая – на третью, а третья – на первую. Через какое время черепахи встретятся, и какое расстояние они пройдут до встречи? [ ]

5.18. Прямая y = 2x начинает двигаться со скоростью v вдаль оси y. С какой скоростью движется точка пересечения этой прямой с осью x? [v_x = v/2]

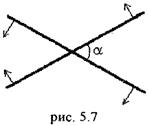
5.19. Две прямые, пересекающиеся под углом a, движутся с одинаковыми по модулю скоростями v в направлениях, перпендикулярных сами себе (рис 5.7). С какой скоростью движется точка их пересечения? [ ]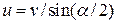

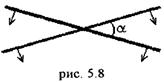
5.20. Решить задачу № 5.19, если скорости прямых направлены как на рис. 5.8.

[ ]

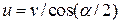5.21. Из двух точек, расположенных на одной высоте и на расстоянии l друг от друга, одновременно бросают два тела: одно вертикально вверх со скоростью v₁; другое горизонтально со скоростью v₂ в направлении первого тела. Найти наименьшее расстоянии между телами. [ ]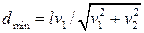

5.22. Из точки B бросают камень в горизонтальном направлении BC с начальной скоростью v_o = 10 м/с. Одновременно из точки A, лежащей на 10 м выше горизонтали BC начинает свободно падать второй камень (рис. 5.9). Через какое время расстояние между камнями будет минимальным и чему оно равно? Расстояние BC = 10 м. [1 c; 10 м]

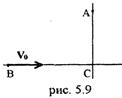5.23. Из одной и той же точки одновременно бросают два камня с одинаковыми начальными скоростями v_o = 10 м/с: один – вертикально вверх, другой – под углом a = 30° к горизонту. Определить расстояние между камнями через t = 2 с после броска. [20 м]

5.24. По грязной дороге едут друг за другом две машины со скоростью v. При каком минимальном расстоянии между машинами грязь, срывающаяся с колес передней машины, не будет попадать на заднюю? Считать, что в момент отрыва скорость комков грязи равна скорости соответствующей точки колеса. Радиус колеса считать малым по сравнению с дальностью полета грязи. [ ]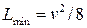

5.25. Магнитофонная лента сматывается с бобины с постоянной скоростью v. Найти зависимость радиуса ленты на бобине от времени, если начальный радиус R_o, а толщина ленты d << R_o. [ ]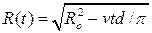

5.26. Два тела одновременно брошены из одной точки с одинаковыми скоростями v_o под углами a и p/2 – a к горизонту. Как зависит от времени расстояние между телами? [ ]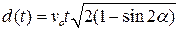

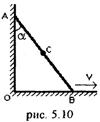5.27. По сторонам прямого угла движется стержень. Конец B стержня движется вправо с постоянной скоростью v (рис. 5.10). Написать зависимость от времени скорости точки A. За начало отсчета принять момент, когда стержень стоял вплотную к вертикальной стене. Определить траекторию движения середины стержня C и скорость точки C в момент, когда угол между стержнем и вертикалью равен a = 45°. Конец A стержня скользит все время по вертикальной стене. Длина стержня l.

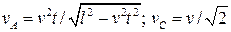[ ; траекторией точки C является окружность с радиусом l/2 с центром в точке O]

5.28. Стержень AB движется произвольным образом. В некоторый момент времени скорость точки A равна v и направлена под углом a к оси стержня, а скорость точки B направлена под углом b к той же оси (рис. 5.11). Определить скорость точки C – середины стержня – в этот же момент. [ ]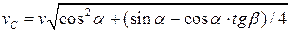

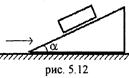5.29. С каким ускорением должна двигаться наклонная плоскость вправо, чтобы не мешать телу свободно падать (рис.5.12)? Угол наклона плоскости – a. [ ]

5.30. Велосипедист, не вращая педалями, движется по горизонтальной окружности. При этом переднее колесо велосипеда движется по окружности радиусом R. Найти радиус окружности, по которой движется заднее колесо, если расстояние между осями колес равно l (R > l). [ . Указание: скорость второго тела направлена вдоль нити и по касательной к окружности]

5.31. Горизонтальная платформа движется со скоростью v. По платформе, с одинаковыми относительно платформы скоростями u, движутся два тела. Скорость одного из них по направлению совпадает с вектором v, а второго – перпендикулярна вектору v. Определить угол между скоростями тел в неподвижной системе отсчета.

[ ]

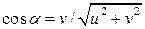5.32. За катером, движущимся со скоростью 30 км/ч, едетспортсмен на водных лыжах (рис. 5.13). Углы между векторами скоростей катера и лыжника и тросом равны: a = 150°; b = 60°. Определить скорость лыжника. [52 км/ч]

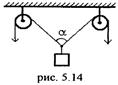
5.33. Груз поднимается при помощи двух неподвижных блоков. Определить скорость груза в момент, когда угол между нитями равен a, если нити вытягиваются с одинаковыми и постоянными скоростями v (рис. 5.14). [ ]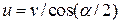

5.34. Груз поднимается при помощи двух неподвижных и одного подвижного блоков. Определить скорость груза в момент, когда угол между нитями равен а, если нити вытягиваются со скоростями u и v (рис. 5.15). [ . Указание: сумма проекций среднего блока на левую и правую нити 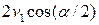равна скорости убывания длины нити между крайними блоками]

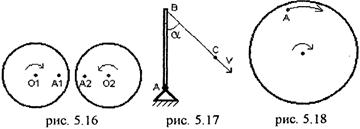5.35. Две расположенные рядом платформы вращаются в противоположных направлениях с одинаковыми угловыми скоростями w = 1 с^–1. В точках A₁ и A₂ стоят два наблюдателя. Известно: O₁O₂ = 5 м; O₁A₁ = O₂A₂ = 2 м. Найти скорость наблюдателя A₁ относительно наблюдателя A₂ в указанный на рис. 5.16 момент времени. [1 м/с. Указание: в системе наблюдателя A₂ весь окружающий мир вращается вокруг него с угловой скоростью w по часовой стрелке]

5.36. Стержень AB приводится в движение нитью BC (рис. 5.17). Когда стержень проходит вертикальное положение скорость точки C равна v, а угол между нитью и стержнем – a. Найти скорость точки B в этот момент. [ ]

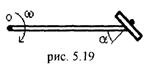5.37. Горизонтальная платформа равномерно вращается вокруг вертикальной оси. По краю платформы с постоянной скоростью идет человек A (рис. 5.18). Ускорение человека относительно платформы равно 0,5 м/с², а переносное ускорение точек края платформы – 2 м/с². Найти абсолютное ускорение человека. [4,5 м/с²]

5.38. Горизонтальный стержень длиной l вращается вокруг вертикальной оси O с угловой скоростью w (рис 5.19). На движущийся конец стержня насажено колесо радиусом r. Угол между осью колеса и стержнем равен a, а само колесо катится по горизонтальному столу. Найти угловую скорость вращения колеса. [ 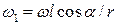. Указание: если бы колесо не вращалось, то точки колеса, соприкасающейся с поверхностью стола, была бы равна . Разложим эту скорость на составляющие: v₁ – параллельная плоскости колеса; v₂ – параллельная оси колеса (рис.). За счет вращения сила трения гасит составляющую скорости v₁.]

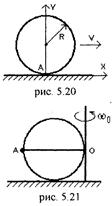5.39. Колесо радиусом R катится без проскальзывания с постоянной скоростью v по горизонтальной поверхности. Приняв положение точки A на рис. 5.20 за начальное, написать зависимости ее координат X_A и Y_A от времени.

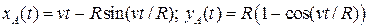[ . Указание: движение точки A можно представить как сумму поступательного движения с постоянной скоростью v и вращательного вокруг центра колеса с угловой скоростью v/R.]

5.40. Шар может свободно вращаться вокруг горизонтального стержня OA, который, в свою очередь, вращается с угловой скоростью w_o вокруг вертикальной оси (рис. 5.21). Определить угловую скорость вращения шара, если проскальзывания нет. [ 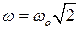. Указание: прямая, проходящая через точку O и точку касания шара с поверхностью является мгновенной осью вращения.]