Управляющие элементы интерфейса и область ввода исходных

данных; 2 – область задания и отображения найденных

коэффициентов автопилота; 3 – область отображения графической информации данных переходного процесса; 4.1,4.2 – области

Построения ЛАФЧХ контура управления

Таким образом, применение данного ПО позволяет сократить время проектирования САУ и подобрать значения коэффициентов автопилота.

Список литературы

1. Распопов В.Я., Товкач С.Е. Авионика малоразмерных беспилотных летательных аппаратов // Мир авионики, 2009 г, №3. – С. 39 - 47.

2. Расчетный и лабораторный практикум по микросистемной авионике: учебное пособие для вузов/под ред. проф., д-ра техн. наук В.Я. Распопова. Тула: Изд-во ТулГУ, 2011. 211 с.

A. V. Ladonkin, M. N. Mashnin

THE SYSTEM FOR AVTOMATED DEFINITION AND CORRECTION
THE COEFFICENTS OF THE AUTOPILOT FOR UNMAINED AIRCRAFT SYSTEMS

The system on the basis requirement of transient process for automatic design
of autopilot’s coefficients on control channels is described in this work.

Key words: the autopilot, the unmanned aircraft system, the autopilot’s coefficients, the airspeed, software.

Получено 09.11.11

УДК 621.9.06

В.А. Крюков, д-р техн. наук, проф., (4872)-33-23-80, krukov@tula.net,
(Россия, Тула, ТулГУ),

Е.Н. Фролович, д-р техн. наук, советник генерального директора
(Россия, Климовск, ОАО «КБАЛ им. Л.Н. Кошкина)

СИНХРОНИЗАЦИЯ ДВИЖЕНИЯ РАБОЧИХ МАШИН
С ПОМОЩЬЮ ЦЕПНОГО КОНВЕЙЕРА

Рассмотрена возможность синхронизации движения рабочих машин автоматических роторных линий с помощью цепного конвейера. Определены силы натяжения в ветвях конвейера. Проанализировано влияние параметров линии и цепного транспортного конвейера на величины сил натяжения в его ветвях.

Ключевые слова: автоматические роторные линии, передачи цепные, динамика, синтез, синхронизация.

Устранение существенного недостатка применяемых в настоящее время схем электромеханического привода автоматических роторных линий, заключающегося в существовании жесткой кинематической связи рабочих роторов, на основе цепного дифференциального конвейера с несколькими степенями свободы и индивидуальных приводов рабочих машин, синхронное движение которых осуществляется с помощью системы автоматического управления, является наиболее универсальным [1]. Однако в некоторых случаях (в линиях малой протяженности, при использовании рабочих машин с малыми нагрузками) может оказаться экономически нецелесообразным. Более простым решением в этом случае является использование цепного дифференциального конвейера с синхронизацией движения рабочих машин за счет сил натяжения в ветвях этого конвейера. На рис. 1 приведен простейший вариант предлагаемого решения для линии, состоящей из двух рабочих машин.

Цепной дифференциальный конвейер 4 охватывает рабочие машины 3, 12, две вспомогательные звездочки с неподвижными осями вращения 6, 11 и две звездочки с подвижными осями вращения 7, 10, подпружиненные пружинами 5, 9 относительно станины 8. Привод линии имеет два электродвигателя 1, 14 и два дифференциальных редуктора (ДР) 2, 13 с двумя степенями свободы каждый. Первый вход каждого редуктора соединен с соответствующим двигателем, выходы редукторов связаны с рабочими машинами. Вторые входы редукторов связаны между собой уравнительной реактивной связью 15, предназначенной для выравнивания нагрузок на выходах редукторов. Рассматриваемая механическая система будет иметь две степени свободы, что позволяет рабочим машинам двигаться независимо друг от друга и обеспечивает развязку движения рабочих машин при аварийной остановке одного из роторов. При нормальном функционировании линии появляющееся рассогласование рабочих машин приводит к перераспределению сил натяжения в цепи, что, в свою очередь, вызывает изменение угловых скоростей роторов и устранение этого рассогласования. Таким образом, обеспечивается необходимое согласование рабочего и транспортного движений.

Увеличение нагрузок на цепной конвейер может привести к его преждевременному выходу из строя. Поэтому при проектировании привода необходимо иметь возможность рассчитывать силы натяжения ветвей цепи в различных режимах движения. Ниже рассматривается решение этой задачи в основном - рабочем (установившемся) режиме движения линии.

Для получения зависимости между моментами на входе и выходе дифференциальных редукторов рассмотрим статику привода линии (рис. 2). Примем, что в приводе используются одинаковые редукторы. Тогда кинематика дифференциальных редукторов будет описываться системой уравнений

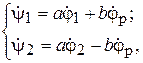
где – углы поворота входных звеньев редуктора; – угол поворота реактивной связи; – углы поворота выходных звеньев редукторов и связанных с ними рабочих машин; – передаточные отношения дифференциальных редукторов.

Рис. 1. Структурная схема привода с синхронизацией движения
роторов с помощью цепного дифференциального конвейера

Рис. 2. Расчетная схема системы дифференциальных редукторов

Обозначая моменты, развиваемые двигателями 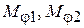, а моменты, приложенные к выходам редукторов со стороны рабочих машин - , и применяя принцип возможных перемещений, получим, что распределение моментов на выходах редукторов при одном и двух включенных двигателях одинаково

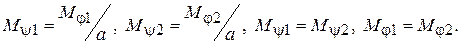
Расчетная схема цепного дифференциального конвейера приведена на рис. 3. Неподвижные звездочки не оказывают влияния на распределение сил в ветвях конвейера и введены для получения его необходимой конфигурации. Для выявления влияния только особенностей рассматриваемой схемы на перераспределение сил в ветвях конвейера в первом приближении будем считать цепь абсолютно гибкой упругой нитью, звездочки заменим круглыми шкивами и примем, что форма ветвей гибкого звена на участках между шкивами прямолинейна [2].

Введем обозначения: – радиусы роторов; – радиусы подвижных звездочек; – коэффициент упругости гибкого звена;
– коэффициенты упругости пружин, связывающих оси подвижных звездочек со станиной; – натяжения в ветвях гибкой связи, причем ; – углы поворота подвижных звездочек.

Поступательное перемещение осей подвижных звездочек определим координатами , отсчитываемыми от положения статического равновесия звездочек в ненагруженном конвейере. Моменты, действующие на рабочих машинах, представим в виде

где – моменты сил технологического сопротивления.

Для определения деформаций упругих звеньев и сил упругости в них (при отсутствии внешних нагрузок) воспользуемся условием [3]

(1)

где 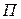– потенциальная энергия системы; – обобщенные координаты, в качестве которых примем .

Преобразуя (1), будем иметь

где – деформации пружин подвижных звездочек в положении статического равновесия; – деформации ветвей гибкой связи в положении статического равновесия.

Рис. 3. Расчетная схема цепного дифференциального конвейера

Отсюда видно, что силы натяжения во всех ветвях гибкой связи одинаковы. Обозначая эти силы 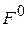, получим значения сил упругости пружин ненагруженного конвейера в виде:

Для определения перемещений элементов системы и величин сил упругости при нагружении рабочих машин моментами воспользуемся уравнениями [3]:

(2)

где – обобщенные силы.

В рассматриваемой системе обобщенные силы будут действовать только по координатам , Остальные обобщенные силы равны нулю: .

В режиме установившегося движения

(3)

что является необходимым условием нахождения цепного конвейера в равновесии.

При выполнении условия (3), система уравнений (2) будет линейно зависимой, т.е. формально может иметь бесконечное множество решений. Для получения одного решения задаем значение одной из координат, например, , что равносильно заданию начала отсчета угловых координат.

Решая систему (2) относительно обобщенных координат и представляя силы натяжения в ветвях гибкой связи в ви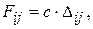де где
– деформации ветвей гибкой связи, которые можно выразить через обобщенные координаты системы

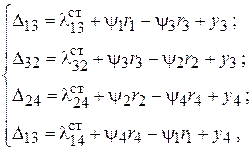
получим зависимости для определения сил натяжения в ветвях конвейера

Для анализа влияния моментов, приложенных к роторам, на перераспределение сил в системе представим силы натяжения цепи следующим образом

где

Переходя к безразмерным величинам, получим

(4)

Здесь – приращение силы натяжения в ведущей ветви недеформируемого конвейера, вызываемое действием крутящего момента ; .

Графики зависимостей при различных значениях параметра приведены на рис. 4. Анализ зависимостей (4) и приведенных графиков позволяет сделать следующие выводы:

1. При работе линии под нагрузкой силы натяжения в ветвях цепного конвейера зависят от жесткости цепи и пружин.

2. Для любых коэффициентов упругости пружин .

3. Если коэффициенты упругости пружин имеют одинаковый порядок , то .

4. При увеличении параметра , что соответствует увеличению жесткости пружин по сравнению с жесткостью цепи, ;

5. При одинаковых пружинах и не зависят от их коэффициентов упругости.

Рис. 4. Влияние упругих характеристик привода на распределение сил
в ветвях цепного конвейера

6. Если жесткость пружин мала по сравнению с жесткостью цепи , то и практически не зависят от жесткости цепи и могут быть определены по приближенным формулам: .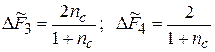

Список литературы

1. Крюков В.А., Прейс В.В. Системы приводов рабочих движений автоматических роторных и роторно-конвейерных линий / Вестник машиностроения. 2003. № 1. С. 36-41.

2. Куровский Ф.М. Теория плоских механизмов с гибкими связями. М.: Машгиз, 1963. 204 с.

3. Добронравов В.В. Основы аналитической механики. М.: Высшая школа, 1976. 264 с.

V.A. Krukov, E.N. Frolovich

SYNCHRONIZATION OF MOVEMENT OF WORKING MACHINES BY MEANS OF THE CHAIN CONVEYOR

Possibility of synchronization of movement of working machines of automated rotor-type transfer lines by means of the chain conveyor is considered. Forces of a tension in the conveyor flights are defined. Influence of parameters of a line and the chain conveyor on tension forces in its flights is analyzed.

Key words: automated rotor-type transfer line, chain transmission, dynamics, synthesis, synchronization.

Получено 20.12.11

УДК 621.9.06

В.А. Крюков, д-р техн. наук, проф., (4872)-33-23-80, krukov@tula.net,
(Россия, Тула, ТулГУ)

ОПТИМИЗАЦИЯ ДИНАМИЧЕСКИХ ПРОЦЕССОВ
В ЦЕПНЫХ ТРАНСПОРТНЫХ КОНВЕЙЕРАХ
АВТОМАТИЧЕСКИХ РОТОРНО-КОНВЕЙЕРНЫХ ЛИНИЙ

Рассмотрены особенности кинематики цепных транспортных конвейеров автоматических роторных линий при малых межосевых расстояниях. Получены уточненные зависимости, позволяющие уменьшить коэффициент неравномерности движения и оптимизировать динамические процессы в линии.

Ключевые слова: автоматические роторные линии, передачи цепные, динамика, синтез.

Переход от автоматических роторных к автоматическим роторно-конвейерным линиям (АРКЛ), способным обеспечить достижение более высокого уровня автоматизации и производительности, привел к появлению в линиях цепного транспортного конвейера. Характерной особенностью цепных передач, к которым относится и указанный конвейер, является непостоянство передаточного отношения, причиной чего служит хордальное расположение звеньев цепи на зубьях звездочки и рассогласование начала входа первого звена ветви цепи в зацепление с ведущей звездочкой и выхода последнего звена ветви из зацепления с ведомой звездочкой [1].

При использовании в качестве системы синхронизации движения роторов зубчатых передач эта особенность приводит к дополнительным нагрузкам на цепной конвейер и его быстрому выходу из строя. Если синхронизация движения осуществляется только с помощью цепного конвейера, то неравномерность движения будет накапливаться при переходе от ротора к ротору и, в конце концов, может достигнуть недопустимых значений. Переменное передаточное отношение также приводит к появлению дополнительных динамических нагрузок на элементы цепного конвейера, что снижает долговечность и надежность линии и отрицательно сказывается на качестве ее работы. Поэтому особую важность имеет определение неравномерности движения ведомых звеньев цепной передачи и разработка методов ее уменьшения.

Используемые в настоящее время методики исследования кинематики и проектирования цепных передач [2, 3, 4] ориентированы на цепные передачи общего машиностроения. Характерными особенностями таких передач являются большие межосевые расстояния [2] , где
– шаг цепи и, соответственно, большое число звеньев цепи в ветвях передачи. При таких значениях геометрических параметров передачи ветви цепи практически не поворачиваются относительно первоначального положения, что позволяет считать их движение поступательным. Это значительно упрощает кинематический анализ передачи и в то же время позволяет получить результаты с приемлемой для практики точностью.

В цепных конвейерах АРКЛ, отличающихся малыми межосевыми расстояниями и малым числом звеньев в ветвях цепи (как правило, не более 4 – 5 звеньев), такой подход может привести не только к количественным погрешностям, но и качественно неверным результатам. Еще одной особенностью цепного конвейера АРКЛ является наличие многозвенных цепных контуров и расположение смежных звездочек снаружи цепного контура. Схему, соответствующую расположению звездочек внутри цепного контура (рис. 1, а), назовем сборкой 1, а схему, соответствующую расположению смежных звездочек снаружи цепного контура – сборкой 2 (рис. 1, б).

А б

Рис. 1. Расположение звездочек цепного конвейера:
а – сборка 1; б – сборка 2

Для получения передаточного отношения участка цепной передачи, состоящей из двух звездочек, ее можно рассматривать (в пределах поворота ведущей звездочки на один угловой шаг) как шарнирный четырехзвенник (рис. 2), в котором ведущая звездочка заменена кривошипом 1 радиусом 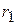, ведомая – кривошипом 2 радиусом , а ведущая ветвь цепи – шатуном длиной , причем число звеньев цепи , содержащихся в рассматриваемой ветви AB обязательно должно быть целым [2]. Радиусы кривошипов являются радиусами делительных окружностей звездочек и рассчитываются по формулам

где – половина углового шага звездочки 1 и 2, соответственно; 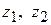– числа зубьев звездочек.

Кроме того, обозначим: - проекции межосевого расстояния 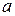на оси координат (см. рис. 2); - углы поворота кривошипов и , проведенных из центров вращения звездочек в центры шарниров цепи, находящихся в зацеплении с ведущей и ведомой звездочками; 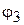- угол поворота шатуна .

В общем случае при вход и выход шарниров цепи в зацепление с зубьями ведущей и ведомой звездочек будет происходить не одновременно. Так для схемы, показанной на рис. 2, ведущая ветвь цепи будет последовательно занимать положения . Это приводит к тому, что число звеньев ветви цепи будет меняться во время движения и, следовательно, являться некоторой неизвестной пока функцией от угла поворота ведущей звездочки.

Для получения функции положения заменяющего шарнирного четырехзвенника запишем уравнение замкнутого векторного контура (см. рис. 2)

и спроецируем его на оси координат

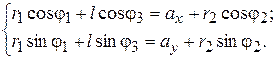(1)

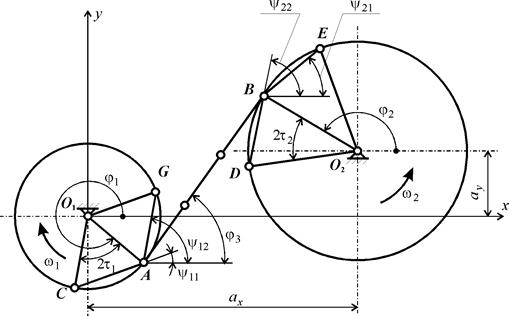
Рис. 2. Определение передаточного отношения цепной передачи

Из рис. 2 видно, что условие зацепления цепи со звездочкой 1 в шарнире 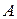будет иметь вид

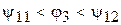, (2)

а условие зацепления цепи со звездочкой 2 в шарнире

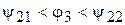. (3)

Выражая из треугольников вспомогательные углы через углы поворота звездочек и их угловые шаги и подставляя найденные зависимости в (2), (3), получим

(4)

Система уравнений и неравенств (1), (4), дополненная уравнением, связывающим неизвестное число звеньев в ветви цепи с ее длиной

, (5)

позволяет определить функцию положения шарнирного четырехзвенника, а, следовательно, и цепной передачи. Указанная система является нелинейной и, кроме того, содержит целочисленную переменную . Поэтому ее решение может быть выполнено только численными методами.

Угол поворота звездочки 1 в системе уравнений (1) изменяется в пределах . В момент входа шарнира 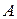в зацепление, определяемый углом , хорда и ветвь должны располагаться на одной прямой, т.е.

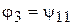. (6)

Аналогично, пересопряжение цепи на звездочке 2, будет определяться углом , удовлетворяющим условию

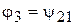. (7)

Решая системы уравнений и неравенств (1), (3), (5), (6) и (1), (2), (5), (7), можно определить значения углов и , соответственно.

Дифференцируя уравнения (1) по времени и выполняя необходимые преобразования, найдем передаточные отношения (первые передаточные функции) рассматриваемой системы

а затем угловые скорости звездочки 2 и ветви цепи

Коэффициент неравномерности угловой скорости звездочки 2

или

где 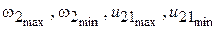– максимальное и минимальное значения угловой скорости звездочки и передаточного отношения, соответственно.

Анализ кинематики цепного контура с двумя звездочками на основе полученных аналитических зависимостей выполнялся численными методами с помощью пакета программ MathСad. Результаты этого анализа представлены на рис. 3-5.

График на рис. 3 иллюстрирует типичную зависимость передаточного отношения (а, следовательно, и угловой скорости ведомой звездочки ) от угла поворота ведущей звездочки в пределах ее поворота на один угловой шаг. Как видно из рисунка, колебания передаточного отношения составляют примерно 8 % от его среднего значения, причем в отличие от известных графиков [3], построенных на основе приближенных зависимостей, он несимметричен относительно середины углового шага, а пересопряжения зацепления на звездочках приводят к изменению числа звеньев в ветви цепи.

Рис. 3. Зависимость передаточного отношения цепной передачи
от угла поворота ведущей звездочки

Рис. 4. Зависимость коэффициента неравномерности движения от

Согласно выполненным ранее исследованиям [2] наименьшее значение коэффициента неравномерности, обеспечивающее оптимальное протекание динамических процессов в передаче, соответствует так называемому синфазному движению звездочек, при котором общая касательная, проведенная к делительным окружностям смежных звездочек , кратна шагу цепи. Исследование зависимости коэффициента неравномерности движения ведомой звездочки от , выполненное на основе уточненных зависимостей (см. рис. 4), показало, что при малых межосевых расстояниях передачи с синфазным движением звездочек не являются оптимальными. Так, для рассмотренных примеров наименьшее значение коэффициента неравномерности обеспечивается при , причем разность между наименьшим значением коэффициента неравномерности и значением этого коэффициента для синфазной передачи ( ) достигает 15 %.

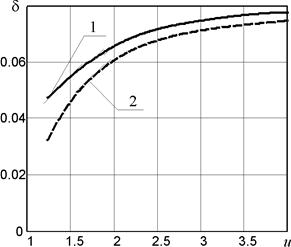
Рис. 5. Зависимость минимально возможного коэффициента
неравномерности движения от передаточного отношения

Анализ зависимости коэффициента неравномерности от передаточного числа передачи при постоянных числе зубьев меньшей звездочки и межосевом расстоянии 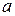(см. рис. 5) показал, что увеличение передаточного числа приводит к увеличению минимально возможного значения коэффициента неравномерности (кривая 2). Эта тенденция справедлива и для синфазной передачи (кривая 1) [2]. Однако в области малых передаточных чисел 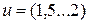выбор значения (а, следовательно, и межосевого расстояния) на основе уточненных зависимостей позволяет существенно уменьшить коэффициент неравномерности движения.

Список литературы

1. Машиностроение. Энциклопедия / Ред. совет: К.В. Фролов (пред.) и др. М.: Машиностроение. Детали машин. Конструкционная прочность. Трение, износ, смазка. Т. IV-1 / Д.Н. Решетов, А.П. Гусенков, Ю.Н. Дроздов и др.; Под общ. ред. Д.Н. Решетова. 1995. 864 с.

2. Готовцев А.А., Котенок И.П. Проектирование цепных передач. М.: Машиностроение, 1982. 336 с.

3. Воробьев Н.В. Цепные передачи. М.: Машиностроение, 1968. 252 с.

4. Глущенко И.П., Петрик А.А. Цепные передачи. Киев: Техника, 1973. 104 с.

V.A. Krukov

Optimization of Dynamic Processes in Chain Transport Conveyors of Automated Rotor-type Transfer Line

Features of kinematics of automated rotor-type transfer lines chain transport
conveyors at small interaxial distances are considered. The specified improved dependences are received. These dependences allow to reduce factor of non-uniformity of movement and to optimize dynamic processes in a line.

Key words: automated rotor-type transfer line, chain transmission, dynamics,
synthesis.

Получено 20.12.11 г.

УДК 621.86.067.3

Н.А. Усенко, д-р техн. наук, проф., (4872)33-23-50, atuzyn@yandex.ru,

(Россия, Тула, ТулГУ),

Чан Минь Тхай, асп., (4872) 33-23-50, lanhdientu1981@yahoo.com,

(Россия, Тула, ТулГУ),

Ле Динь Шон, асп., +79654081040, ledinhson@mail.ru,

(Россия, Тула, ТулГУ),

Р.И. Клейменов, асп., (4872) 33-23-50, romankleimenov@yandex.ru,

(Россия, Тула, ТулГУ)