
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Структурные средние.
Для характеристики структуры вариационных рядов применяются так называемые структурные средние. Наиболее часто используются в экономической практике мода и медиана.
Мода - это наиболее часто встречающаяся варианта признака в данной совокупности.
В дискретных вариационных рядах мода определяется по наибольшей частоте. Предположим товар «А» реализуют в городе 9 фирм по цене в рублях:
44; 43; 44; 45; 43; 46; 42; 46;43;
Так как чаще всего встречается цена 43 рубля, то она и будет модальной.
В интервальных вариационных рядах моду определяют приближенно по формуле
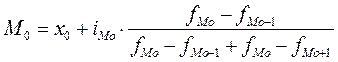 , где
, где
x0 - нижняя граница модального интервала;
 - величина модального интервала;
- величина модального интервала;
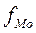 - частота модального интервала;
- частота модального интервала;
 - частота интервала, предшествующая модальному;
- частота интервала, предшествующая модальному;
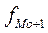 - частота интервала, следующая за модальным.
- частота интервала, следующая за модальным.
Место нахождения модального интервала определяют по наибольшей частоте (таблица 5.3)
Таблица 5.3.
Распределение населения РФ по уровню среднедушевого месячного дохода в I-ом полугодии 1995 года
| Среднедушевой месячный доход, руб. | Удельный вес населения, % (f i) | Накопленная частота, % (Si) |
| менее 100 100-300 300-500 500-700 700-900 900 и выше | 2,4 35,5 30,0 15,7 7,7 8,7 | 2,4 37,9 67,9 83,6 91,3 100,0 |
| Всего | 100,0 | Х |
Интервал 100-300 в данном распределении будет модальным, т.к. он имеет наибольшую частоту ( 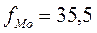 ). Тогда по вышеуказанной формуле мода будет равна:
). Тогда по вышеуказанной формуле мода будет равна:
 руб.
руб.
Мода применяется для решения некоторых практических задач. Так, например, при изучении товарооборота рынка берется модальная цена, для изучения спроса на обувь, одежду используют модальные размеры обуви и одежды и др.
Медиана - это численное значение признака у той единицы совокупности, которая находится в середине ранжированного ряда (построенного в порядке возрастания, либо убывания значения изучаемого признака). Медиану иногда называют серединной вариантой, т.к. она делит совокупность на две равные части. В дискретных вариационных рядах с нечетным числом единиц совокупности - это конкретное численное значение в середине ряда. Так в группе студентов из 27 человек медианным будет рост у 14-го, если они выстроятся по росту. Если число единиц совокупности четное, то медианой будет средняя арифметическая из значений признака у двух средних членов ряда. Так, если в группе 26 человек, то медианным будет рост средний 13-го и 14-го студентов. В интервальных вариационных рядах медиана определяется по формуле:
 , где x0 - нижняя граница медианного интервала;
, где x0 - нижняя граница медианного интервала;  - величина медианного интервала;
- величина медианного интервала; 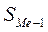 - сумма накопленных частот до медианного интервала; fMe - частота медианного интервала. По данным таблицы 5.3. определим медианное значение среднедушевого дохода. Для этого необходимо определить, какой интервал будет медианным. Используя формулу накопленной частоты до медианы, т.е. середины
- сумма накопленных частот до медианного интервала; fMe - частота медианного интервала. По данным таблицы 5.3. определим медианное значение среднедушевого дохода. Для этого необходимо определить, какой интервал будет медианным. Используя формулу накопленной частоты до медианы, т.е. середины 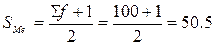 (%) .
(%) .
Дробное значение SМе (всегда при четном числе членов) равное 50,5% говорит о том, что середина ряда находится между 50% и 51%, т.е. в третьем интервале. Отсюда медиана по формуле будет определена.
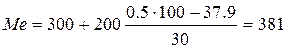 руб.
руб.
Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если M0<Me< 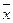 имеет место правосторонняя асимметрия. Если же
имеет место правосторонняя асимметрия. Если же 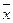 <Me<M0 - левосторонняя асимметрия ряда. По приведенному примеру можно сделать заключение, что наиболее распространенным является доход порядка 271 руб. в месяц. В то же время более половины населения располагают доходом свыше 381 руб., при среднем уровне 435 руб.
<Me<M0 - левосторонняя асимметрия ряда. По приведенному примеру можно сделать заключение, что наиболее распространенным является доход порядка 271 руб. в месяц. В то же время более половины населения располагают доходом свыше 381 руб., при среднем уровне 435 руб. 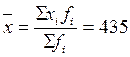 руб. Из соотношения этих показателей следует сделать вывод о правосторонней асимметрии распределения населения по уровню среднедушевого денежного дохода.
руб. Из соотношения этих показателей следует сделать вывод о правосторонней асимметрии распределения населения по уровню среднедушевого денежного дохода.
Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные (по числу единиц) части - квартили, на десять частей - децили, на сто частей - перцентили. Так формула первого квартиля будет 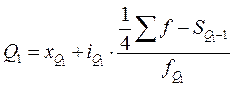 . Второй квартиль равен медиане. Формула третьего квартиля будет
. Второй квартиль равен медиане. Формула третьего квартиля будет 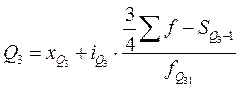 .
.
Аналогичны формулы децилей. Пятый дециль равен медиане.
Среди множества варьирующих признаков существуют признаки, которыми одни единицы совокупности обладают, а другие не обладают. Такие признаки называются альтернативными. Примером таких признаков являются: наличие бракованной продукции, ученая степень у преподавателя, наличие академической задолженности у студента и др. Обозначим: 1 — наличие интересующего нас признака; 0 — его
отсутствие; р — доля единиц, обладающих данным признаком; q — доля единиц, не обладающих данным признаком; тогда р+q=1.
Дата добавления: 2014-11-13; просмотров: 336; Мы поможем в написании вашей работы!; Нарушение авторских прав |