
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Среднее квадратическое отклонение альтернативного признака
σp = 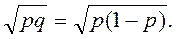
В статистической практике часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для подобных сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях.
Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различной средней арифметической используют относительные показатели вариации
Относительные показатели вариации определяются как отношение абсолютных показателей вариации к средней арифметической.
Это коэффициент осцилляции, определяемый как отношение размаха вариации к средней арифметической величине в процентах 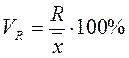 .
.
Линейный коэффициент вариации определяется аналогично, но по среднему линейному отклонению 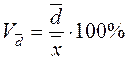 .
.
Наиболее распространенными из них являются коэффициент вариации.
Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
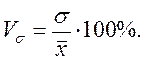
Относительные показатели вариации характеризуют степень колеблемости признака внутри средней величины. По величине, например, коэффициента вариации можно определить степень однородности изучаемой совокупности. Совокупность считается достаточно однородной, если коэффициент вариации не превышает 33%. Для оценки качества, устойчивости средней величины установлены пределы. Самыми лучшими значениями коэффициента вариации являются 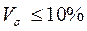 ; допустимыми считаются значения до 50%.
; допустимыми считаются значения до 50%.
6.3. Свойства дисперсии и упрощенные методы ее расчета.
Техника вычисления дисперсии по формулам достаточно сложна, а при больших значениях вариантов и частот может быть громоздкой. Расчет можно упростить, используя свойства дисперсии (доказываемые в математической статистике):
Первое свойство — если все значения признака уменьшить на одну и ту же постоянную величину А, то дисперсия от этого не изменится;
σ2(х-А)=σх2
Второе свойство— если все значения признака уменьшить в одно и то же число i раз, то дисперсия соответственно уменьшится в i2 раз.
σ2(х/i)=σx2:i2
Третье свойство (свойство минимальности) - средний квадрат отклонений
от любой величины А (отличной от средней арифметической) больше
дисперсии признака на квадрат разности между средней арифметической и величиной А
 |
σA2=σx2+(x-A)2
Используя свойства дисперсии, получим следующую упрощенную формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
σ2= 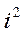 ∙ (
∙ ( 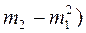

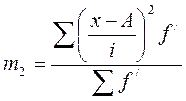 - момент второго порядка
- момент второго порядка
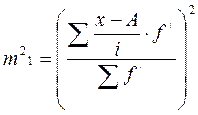 - квадрат момента первого порядка
- квадрат момента первого порядка
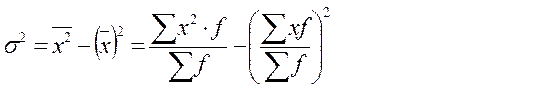 |
На основании последнего свойства дисперсии упрщенная формула дисперсии для любого ряда (дискретного, интервального с равным и неравным интервалами) формула дисперсии примет вид:
6.4. Виды дисперсий.
Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами. В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой.
Общая дисперсия σ2 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака х от общей средней  и может быть вычислена как простая дисперсия или взвешенная дисперсия.
и может быть вычислена как простая дисперсия или взвешенная дисперсия.
Межгрупповая дисперсия  δ2 характеризует систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних
δ2 характеризует систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних 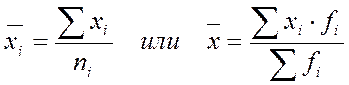 , от общей средней
, от общей средней 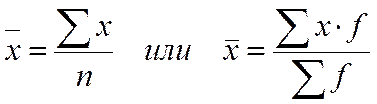
и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
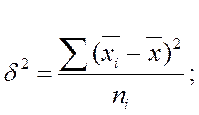
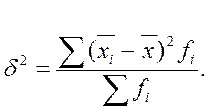
Межгрупповая дисперсия отражает вариацию признака, положенного в основу группировки.
Внутригрупповая (частная) дисперсия (в каждой группе) σi2, отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы 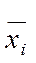 , (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
, (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
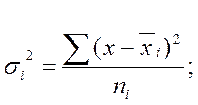
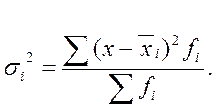
На основании внутригрупповых дисперсий по каждой группе, т.е. на основании σi2 можно определить среднюю из внутригрупповых дисперсий:
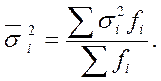
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью - неизвестную, а также судить о силе влияния группировочного признака.
Долю вариации группировочного признака в совокупности характеризует эмпирический коэффициент детерминации 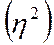 .
.
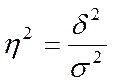
Глава 7.
Выборочное наблюдение.
7.1.Выборочное наблюдение как источник статистической информации.
Под выборочным наблюдением понимается такое несплошное наблюдение, при котором статистическому обследованию подвергаются единицы совокупности, отобранные в случайном порядке.
Переход статистики РФ на международные стандарты требует более широкого применения выборки для получения и анализа показателей во многих секторах экономики. К выборочному наблюдению статистика прибегает по различным причинам. Существование множества субъектов хозяйственной деятельности, которые характерны для рыночной экономики, не позволяет использовать сплошное обследование из-за огромных материальных, финансовых и трудовых затрат. Выборочное наблюдение экономит ресурсы, позволяет расширить программу наблюдения и использовать более квалифицированные кадры для проведения наблюдения. Выборочное наблюдение используют и для решения таких задач, где сплошное наблюдение применять невозможно (изучение качества продукции) или нецелесообразно, а также для уточнения и проверки результатов сплошного наблюдения. В отличие от других видов несплошного наблюдения выборочное наблюдение позволяет получить необходимые сведения приемлемой точности.
Совокупность отобранных для обследования единиц в статистике называют выборочной, а совокупность единиц, из которых производится отбор – генеральной.
Результаты выборочного статистического исследования во многом зависят от уровня подготовки процесса наблюдения. В данном случае подразумевается соблюдение определенных правил и принципов проектирования выборочного обследования. Особенно важным является составление организационного плана выборочного наблюдения. В организационный план включаются следующие вопросы:
1.Постановка цели и задачи наблюдения.
2.Определение границ объекта исследования.
3.Отработка программы наблюдения и разработки ее материалов.
4. Определение процедуры отбора, способа отбора и объема выборки.
5. Подготовка кадров для проведения наблюдения, тиражирование формуляров, инструктивных материалов.
6. Расчет выборочных характеристик и определение ошибок выборки.
6. Распространение выборочных данных на всю генеральную совокупность.
Основные характеристики параметров генеральной и выборочной совокупности обозначаются определенными символами (таблица 7.1.).
Таблица 7.1.
Символы основных характеристик параметров генеральной и выборочной совокупностей.
| Характеристика | Генеральная совокупность | Выборочная совокупность |
| Объем совокупности (численность единиц) | N | n |
| Численность единиц, обладающих обследуемым признаком | M | m |
| Доля единиц, обладающих обследуемым признаком | 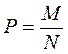
| 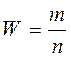
|
| Средний размер признака | 
| 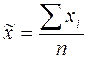
|
| Дисперсия количественного признака | 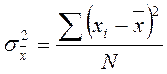
| 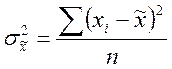
|
| Дисперсия доли | 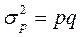
| 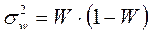
|
7.2. Основные способы формирования выборочной совокупности.
Достоверность рассчитанных по выборочным данным характеристик зависит от способа отбора единиц из генеральной совокупности. В каждом конкретном случае в зависимости от ряда условий выбирают наиболее предпочтительную систему организации отбора, которая определяется видом, методом и способом отбора.
По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности. При групповом отборе отбираются группы единиц. Комбинированный отбор предполагает сочетание индивидуального и группового отбора.
Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора.
Бесповторным называется отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор.
При повторном отборе попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность для участия в дальнейшем отборе. Повторный метод отбора применяется в тех случаях, когда характер исследования предполагает возможность повторной регистрации единиц. Например, в выборочных обследованиях населения в качестве покупателей, избирателей, абитуриентов и т. д.
Способ отбора определяет конкретный механизм выборки единиц из генеральной совокупности. В практике обследований получили распространение следующие виды выборки:
- собственно - случайная;
- механическая;
- типическая;
- серийная;
- комбинированная.
Собственно - случайная выборка заключается в отборе единиц из генеральной совокупности наугад, без какой либо системности. Технически этот отбор проводят методом жеребьевки (использование фишек, шаров, карточек и т.д. в количестве генеральной совокупности) или по таблице случайных чисел (произвольные столбцы цифр).
Собственно-случайный отбор может быть повторным и бесповторным.
После проведения отбора для определения возможных границ генеральных характеристик рассчитывается средняя и предельная ошибки выборки.
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора по формулам:
при повторном отборе 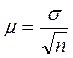 ,
,
при бесповторном отборе 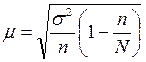 , где
, где
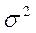 - выборочная (или генеральная) дисперсия;
- выборочная (или генеральная) дисперсия;
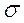 - выборочное (или генеральное) среднее квадратическое отклонение;
- выборочное (или генеральное) среднее квадратическое отклонение;
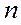 - объем выборочной совокупности;
- объем выборочной совокупности;
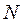 -объем генеральной совокупности
-объем генеральной совокупности
Предельная ошибка выборки связана со средней ошибкой выборки соотношением: 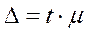 , где
, где
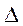 - предельная ошибка выборки;
- предельная ошибка выборки;
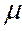 - средняя ошибка выборки;
- средняя ошибка выборки;
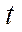 - коэффициент доверия, определяемый в зависимости от уровня вероятности Р.
- коэффициент доверия, определяемый в зависимости от уровня вероятности Р.
Таблица 7.2.
Значения t в зависимости от уровня вероятности.
| Вероятность, Рi | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Так для средней в генеральной совокупности эти пределы будут 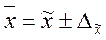 , где
, где
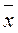 -генеральная средняя;
-генеральная средняя;
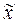 - выборочная средняя;
- выборочная средняя;
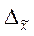 -предельная ошибка для выборочной средней.
-предельная ошибка для выборочной средней.
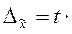
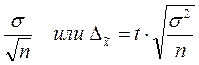 , а при бесповторном отборе
, а при бесповторном отборе 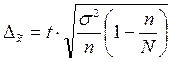 .
.
Эти же показатели могут быть определены и для доли признака. В этом случае особенности расчета связаны с определением дисперсии доли, которая определяется по формуле: 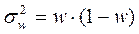 , где
, где 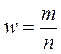 - доля единиц, обладающих признаком в выборочной совокупности.
- доля единиц, обладающих признаком в выборочной совокупности.
Тогда, например, при собственно-случайном отборе для определения предельной ошибки выборки при повторном отборе используется формула:
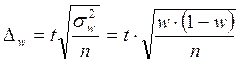 , а при бесповторном отборе
, а при бесповторном отборе
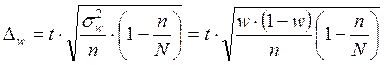 .
.
Пределы доли признака в генеральной совокупности будут
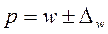 .
.
Механическая выборка применяется в случаях, когда генеральная совокупность упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера, номера домов и т.д.).
Для механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей. Так, если генеральная совокупность 500 000 единиц и предполагается получить 2% выборку, т.е. отобрать 10 000 единиц, то пропорция отбора составит 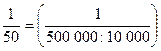 . Отбор осуществляется в соответствии с установленной пропорцией через равные интервалы. Например, при пропорции 1:50 (2% выборка) отбирается каждая 50-я единица.
. Отбор осуществляется в соответствии с установленной пропорцией через равные интервалы. Например, при пропорции 1:50 (2% выборка) отбирается каждая 50-я единица.
Для определения средней ошибки механической выборки используется формула средней ошибки при собственно-случайном бесповторном отборе.
Типический отбор используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. Например, при обследовании населения это могут быть районы, возрастные или образовательные группы и т.д.
Средняя ошибка такой выборки находится по формулам:
при повторном отборе 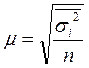 ,
,
а при бесповторном отборе 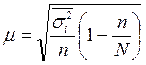 , где
, где
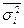 - средняя из внутригрупповых дисперсий.
- средняя из внутригрупповых дисперсий.
Серийный отбор удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:
при повторном отборе 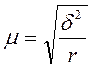 ,
,
а при бесповторном отборе 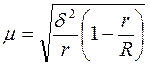 , где
, где
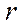 -число отобранных серий (групп);
-число отобранных серий (групп);
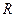 - общее число серий (групп).
- общее число серий (групп).
Межгупповую дисперсию вычисляют по формуле 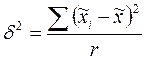 , где
, где
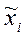 -средняя i-ой серии (группы);
-средняя i-ой серии (группы);
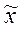 - общая средняя по всей выборочной совокупности.
- общая средняя по всей выборочной совокупности.
7.3. Определение необходимого объема выборки.
При проектировании выборочного наблюдения вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину установленной ошибки, а также на базе способа отбора.
Наиболее часто применяемые на практике формулы объема выборки
для собственно-случайной и механической выборки:
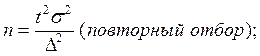
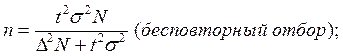
Для типической выборки:
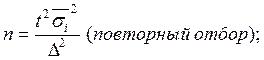
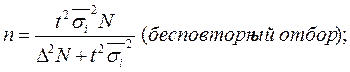
Для серийной выборки:
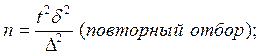
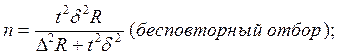
В зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины и для доли признака.
7.4. Малая выборка.
В практике статистического исследования в условиях рыночной экономики все чаще приходится сталкиваться с небольшими по объему так называемыми малыми выборками. Под малой выборкой понимается такое выборочное наблюдение, численность единиц которого не превышает 30.
В настоящее время малая выборка используется более широко, чем раньше за счет статистического изучения деятельности малых и средних предприятий, коммерческих банков, фермерских хозяйств и т. д. Их количество, особенно при региональных исследованиях, а также величина характеризующих их показателей, часто незначительны. Поэтому хотя общий принцип выборочного обследования (с увеличением объема выборки точность выборочных данных повышается) остается, иногда приходится ограничиваться малым числом наблюдений. Необходимость в малой выборке возникает также в научно-исследовательской работе.
При оценке результатов малой выборки величина генеральной дисперсии в расчетах не используется. Для определения возможных пределов ошибки пользуются критерием Стьюдента, определяемым по формуле:
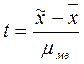 , где
, где 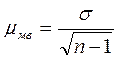 .
.
Глава 8.
Статистические методы выявления взаимосвязи.
8.1.Виды взаимосвязей.
Все явления в природе и обществе находятся во взаимной связи и взаимной обусловленности. Статистика изучает закономерности изменения одних явлений в связи с изменением других.
Народное хозяйство и отдельные предприятия характеризуются системой показателей, образующих диалектическое единство. Эти показатели связаны между собой и порождают друг друга.
Связь явлений имеет разнообразные проявления. Существуют различные формы и виды связей, которые отличаются по существу, характеру проявления, направлению, тесноте, аналитическому выражению и т.д.
По степени зависимости одного явления от другого различают в общем виде два типа связи: связь функциональную (полную) и связь стохастическую (неполную).
Функциональная связь- это связь, где каждому значению одной переменной (аргументу) соответствует одно вполне определенное значение другой переменной (функции). Такие связи широко распространены в технике, биологии, математике, Например, площадь круга определяется однозначно величиной радиуса 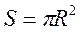 .
.
При стохастической форе связи каждому значению одного признака (факторного) соответствует целый ряд значений другого признака (результативного). Следовательно, стохастическая связь проявляется не в каждом отдельном случае, а лишь в среднем для совокупности явлений данного вида.
Социально - экономические процессы и явления - это результат действия многочисленных факторов. Одни из них поддаются точному измерению, а другие - нет, т.е. их можно измерить только приближенно. Для социально- экономических явлений характерен тот факт, что наряду с факторами, определяющими исследуемую зависимость, действуют многочисленные случайные факторы. Поэтому зависимость проявляется не в каждом отдельном случае, а лишь, в общем, в среднем.
Статистика призвана определять наличие связи между явлениями, ее направление и форму выражения, измерять тесноту этой связи.
8.2. Методы изучения взаимосвязей.
Для изучения связи между явлениями статистика использует ряд методов и приемов, важнейшие из которых: метод приведения параллельных рядов, метод группировок, индексный метод, балансовый метод и группа корреляционных методов.
Метод приведения параллельных рядов заключается в установлении связи между явлениями посредством сопоставления двух или нескольких рядов показателей. Такое сопоставление производится после того, как теоретически доказана возможность связи между изучаемыми показателями. Сопоставление параллельных рядов позволяет установить наличие связи и получить представление о ее характере. Сущность метода параллельных рядов заключается в следующем: факторный признак располагается в возрастающем (или убывающем) порядке и параллельно располагаются соответствующие значения одного или нескольких результативных признаков. Сравнивая, расположенные таким образом ряды показателей, выявляется существование связи и ее направление.
Метод параллельных рядов прост и достаточно эффективен на первых стадиях исследования.
Метод аналитических группировок позволяет не только констатировать наличие связи между изучаемыми признаками, но и выявлять причины этой связи. Чтобы анализировать сложные взаимные связи между несколькими признаками применяются комбинационные группировки. В основе группировки всегда факторный признак. Затем для каждой выделенной группы рассчитываются обобщающие показатели. В итоге рассматривают, какое влияние оказывает факторный признак на результативный. С помощью метода группировок можно рассматривать одновременное действие нескольких признаков – факторов, а также характеризовать структуру совокупности.
Балансовый метод заключается в построении различных балансовых равенств в виде соотношений между наличием и распределением тех или иных ресурсов, ввозом и вывозом и т. д. Простейшим балансом такого рода является баланс материальных ресурсов на предприятии, Здесь балансовое равенство можно записать так:
Остаток на начало периода + поступление = расход + остаток на конец периода. Балансы позволяют выявить взаимосвязи в образовании и распределении ресурсов между предприятиями, районами и т. д., позволяют анализировать сложившиеся пропорции и зависимости. Такого рода балансы распространены в торговле, балансовым методом изучают движение рабочей силы, финансов, основных фондов и т. д. На основе балансов выявляют важные для анализа развития народного хозяйства показатели.
Индексный метод служит для определения роли отдельных факторов в изменении изучаемого явления с целью воздействия на положительно влияющие факторы. Исследование удельного веса факторов опирается на взаимосвязи связанных явлений. Факторный индексный анализ позволяет численно точно определить степень влияния каждого фактора в совместном влиянии факторов.
Корреляционные методы выявления взаимосвязей в отличие от вышеизложенных методов изучения взаимосвязей не только позволяют установить связь и выявить ее причины, но и позволяют измерить степень тесноты связи. Они дают возможность выразить эту связь аналитически в виде определенного математического уравнения. Корреляционные методы анализа являются основными в изучении связей между социально - экономическими явлениями. Корреляционная зависимость исследуется с помощью корреляционного и регрессионного анализов. Корреляционный анализ позволяет оценить тесноту связи с помощью парных, частных и множественных коэффициентов корреляции. Целью регрессионного анализа является оценка функциональной зависимости среднего значения результативного признака (У) от факторного (Х) или факторных
(Х1, Х2, Х3, …Хn).
Корреляционные методы изучения взаимосвязей можно разделить на две группы: непараметрические методы и методы собственно корреляции.
8.3.Непараметрические корреляционные методы изучения взаимосвязей.
Непараметрические корреляционные методы исследования связей включают расчеты различных коэффициентов, с помощью которых измеряется теснота связи между явлениями, где обычные методы корреляции недостаточны или невозможны. Например, при определении тесноты связи между качественными признаками. Непараметрические методы не требуют никаких предположений о законе распределения исходных данных, т. к. при их использовании оперируют не значениями признаков, а их частотами, знаками, рангами и т. д. Это ранговый коэффициент Спирмена, коэффициент Фехнера, коэффициенты ассоциации и контингенции, коэффициенты взаимной сопряженности Пирсона и Чупрова, коэффициент корреляции рангов Кендалла.
Ранговый коэффициент Спирмена измеряет взаимосвязь между отдельными признаками с помощью условной оценки по рангам. Ранг (R) – это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величины на основе предпочтения (лучший – на первом месте, худший – на последнем). Рассчитывается он по формуле:
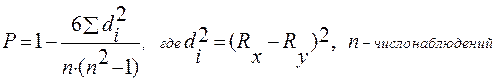
Коэффициент Спирмена изменяется от – 1 до + 1 и равен нулю при отсутствии связи. Эта формула используется, когда нет связанных (одинаковых в ряду) рангов. Если значения признака совпадают (появляются одинаковые в ряду ранги), то определяется средний ранг путем деления суммы рангов на число значений. Коэффициент Спирмена в этом случае определяется по формуле
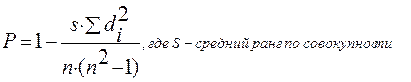 Критерий тесноты связи для коэффициента Спирмена 0,5, т.е. Р≥ 0,5
Критерий тесноты связи для коэффициента Спирмена 0,5, т.е. Р≥ 0,5
Значимость коэффициента Спирмена проверяется на основе критерия Стьюдента. Расчетное значение критерия Стьюдента определяется по формуле 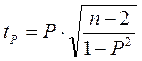 , которое сравнивается с теоретическим
, которое сравнивается с теоретическим
значением (tT) при заданном уровне значимости и числе степеней свободы (n-m). Значение коэффициента корреляции рангов Спирмена считается существенным, если tP› tT .
Коэффициент Фехнера (Кф) или коэффициент совпадения знаков основан на применении первых степеней отклонений от средних значений признаков двух связанных рядов показателей.
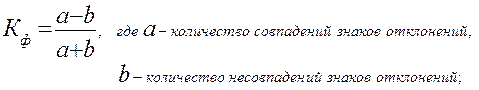
Коэффициент Фехнера также изменяется от -1 до +1 и равен нулю при отсутствии связи. В сравнении с коэффициентом Спирмена он дает более осторожную оценку, т.е. коэффициент Фехнера всегда меньше коэффициента Спирмена.
Коэффициент корреляции рангов Кендалла также используется для измерения тесноты связи между качественными признаками, ранжированными по одному принципу. Расчет осуществляется по формуле:
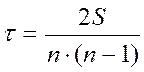 , где n-число наблюдений; S=P+Q.
, где n-число наблюдений; S=P+Q.
Для нахождения P и Q надо произвести ранжирование по факторному признаку (х) в порядке предпочтительности и ранжирование по результативному признаку (у) соответственно предпочтительности факторного признака. Тогда Р - это количество чисел, находящихся после каждого из элементов последовательности рангов переменной (у) и имеющих величину ранга больше ранга рассматриваемого элемента, а Q- это количество чисел находящихся после каждого из элементов последовательности рангов переменной (у), имеющих величину ранга меньше ранга рассматриваемого элемента и взятых со знаком минус.
Например, необходимо определить степень тесноты связи между уровнем механизации труда (х) и трудоемкостью единицы продукции (у) по данным 10 заводов:
Таблица 8.1
| Номер завода | ||||||||||
| Уровень механизации труда, % | ||||||||||
| Трудоемкость единицы продукции, мин. | ||||||||||
| Ранг по х | ||||||||||
| Ранг по у |
Ранг по х проставляется от большего к меньшему, т.к. лучшее значение большее. Ранг по у проставляется в соответствии с ранжированием х ,т.е. тоже от большего к меньшему. Располагаем ранги по х в порядке возрастания, а по у в соответствии с х.
Таблица 8.2
| Номер завода | ||||||||||
| Уровень механизации труда, % | ||||||||||
| Трудоемкость единицы продукции, мин. | ||||||||||
| Ранг по х | ||||||||||
| Ранг по у |
Определяем Р = 0+0+4+0+1+3+3+1+0=12, т.к. после 10 ранга по у нет чисел больше 10 (0), после 9 нет чисел больше 9 (0), после 4 четыре числа больше 4 (8; 6; 5; 7), после 8 нет чисел больше 8 (0), после 6 одно число больше 6 (7), после 2 три числа больше 2 (5; 7; 3), после 1 три числа больше 1 (5; 7; 3), после 5 одно число больше 5 (7), после 7 нет чисел больше 7 (0).
Определяем Q= -9-8-3-6-4- 1-0-1-1=-33, т.к. после 10 девять чисел меньше 10, после 9 восемь чисел меньше 9. после 4 три числа меньше 4 и т. д. Следовательно, 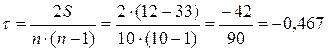 связь умеренная и обратная.
связь умеренная и обратная.
Коэффициент Кендалла изменяется от -1 до + 1 и равен нулю при отсутствии связи.
Если в изучаемой совокупности есть связанные ранги, то расчеты коэффициента Кендалла необходимо произвести по следующей формуле:
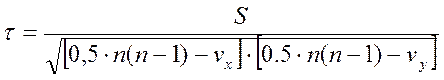 , где
, где
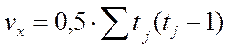 ;
; 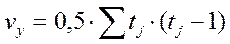 ;
;
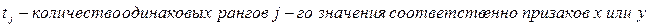
Значимость коэффициента Кендалла также определяется по t критерию Стьюдента.
В практике статистических исследований приходится иногда анализировать связь между альтернативными признаками, представленными только группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценить с помощью коэффициентов ассоциации и контингенции.
Коэффициент ассоциации определяется по формуле
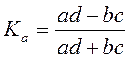 Связь считается подтвержденной, если Ка≥0,5
Связь считается подтвержденной, если Ка≥0,5
Коэффициент контингенции определяется по формуле:
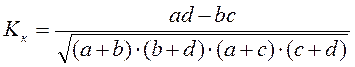
Связь считается подтвержденной, если Кк≥0,3
Для расчета коэффициентов ассоциации и контингенции строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным.
Таблица 8.3
 Группы по признаку у Группы по признаку у
 Группы по признаку х
Группы по признаку х
| Итого | ||
 a a
| b | a+b | |
| c | d | c+d | |
| Итого | a+c | b+d | a+b+c+d |
или
Таблица 8.4
 Группы по признаку (у)
Группы по признаку (х) Группы по признаку (у)
Группы по признаку (х)
| Итого | ||
| a | c | a+c | |
| b | d | b+d | |
| Итого | a+b | c+d | a+c+b+d |
Коэффициент контингенции всегда меньше коэффициента ассоциации, но оба изменяются от -1 до +1.
При ad›bc связь прямая, при ad‹bc связь обратная, при ad=bc связь отсутствует.
Если по каждому из взаимосвязанных признаков число групп больше двух, то теснота связи между качественными признаками измеряется с помощью показателей взаимной сопряженности Пирсона и Чупрова.
Коэффициент взаимной сопряженности Пирсона определяется по формуле 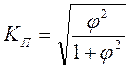 , где
, где 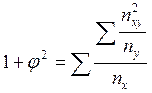 или
или 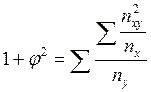
Связь считается подтвержденной, если КП≥0,3
Коэффициент взаимной сопряженности Чупрова определяется по формуле 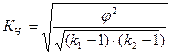 ,
,
где k1- количество групп по признаку х; k2-количество групп по признаку у
Критерий тесноты связи Кч≥ 0,3
Для расчета коэффициентов Пирсона и Чупрова используется таблица, в которой количество групп по каждому признаку может быть более двух.
Таблица 8.5
  Группы по признаку (у)
Группы по признаку (х) Группы по признаку (у)
Группы по признаку (х)
| 2 и т.д. | Итого | |
| nxy | nxy | nx | |
| nxy | nxy | nx | |
| 3 и т. д. | nxy | nxy | nx |
| Итого | ny | ny | n |
Проверка значимости коэффициентов Пирсона и Чупрова осуществляется по критерию 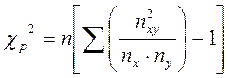 , где nxy-частота совместного появления признаков; nx,ny-суммы частот по строкам и столбцам соответственно; n-численность совокупности. Расчетное значение
, где nxy-частота совместного появления признаков; nx,ny-суммы частот по строкам и столбцам соответственно; n-численность совокупности. Расчетное значение 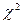 должно быть больше табличного (
должно быть больше табличного ( 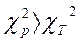 ) при выбранном уровне вероятности. Формулы коэффициентов Пирсона и Чупрова через
) при выбранном уровне вероятности. Формулы коэффициентов Пирсона и Чупрова через 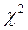 будут соответственно:
будут соответственно:
Коэффициент Пирсона 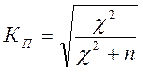 ;
;
Коэффициент Чупрова 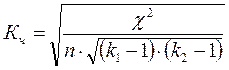 .
.
8.4.Методы собственно-корреляции.
Все явления и процессы, характеризующие социально-экономическое развитие и составляющие единую систему национальных счетов, тесно взаимосвязаны и взаимозависимы между собой.
В статистике показатели, характеризующие эти явления, могут быть связаны либо корреляционной зависимостью, либо быть независимыми.
Корреляционная зависимость является частным случаем стохастической зависимости, при которой изменение значений факторных признаков (х1,х2,…, хn) влечет за собой изменение среднего значения результативного признака.
Корреляционная зависимость исследуется с помощью методов корреляционного и регрессионного анализов.
Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается величиной коэффициентов корреляции.
Основной предпосылкой применения корреляционного анализа является необходимость подчинения значений всех факторных признаков и результативного нормальному закону распределения или близость к нему.
Если объем изучаемой совокупности достаточно большой (n›50), то нормальность распределения может быть подтверждена на основе расчета и анализа, например, критерия Пирсона. Если n‹50, то закон распределения исходных данных определяется на базе построения и визуального анализа поля корреляции (графически).
Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака от факторных признаков. Он заключается в определении аналитического выражения связи.
Основной предпосылкой регрессионного анализа является то, что только результативный признак подчиняется нормальному закону распределения, а факторные признаки могут иметь произвольный закон распределения.
Уравнение регрессии, или статистическая модель связи социально-экономических явлений, выражаемая функцией 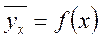 .
.
Теоретическая обоснованность моделей взаимосвязи, построенных на основе корреляционно-регрессионного анализа, обеспечивается соблюдением следующих основных условий:
1. Все признаки должны подчиняться нормальному закону распределения.
2. Отдельные наблюдения должны быть независимыми, т. е. между собой.
Практика выработала определенный критерий в определении оптимального числа факторов. Число факторных признаков должно быть в 5-6 раз меньше объема изучаемой совокупности.
По количеству включаемых факторов модели могут быть однофакторными и многофакторными.
Наиболее разработанной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака х на результативный признак у и представляющая собой однофакторный корреляционный и регрессионный анализ. Овладение теорией и практикой построения и анализа двухмерной модели корреляционного и регрессионного анализа представляет собой исходную основу для изучения многофакторных стохастических связей.
Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. Сложность заключается в том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками.
По форме зависимости различают:
- линейную регрессию, которая выражается уравнением прямой (линейной функцией) 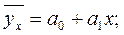
- нелинейную регрессию, которая выражается уравнениями вида:
-гиперболы - 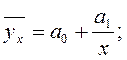
-параболы второго порядка - 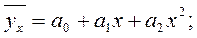 и т. д.
и т. д.
По направлению связи различают:
- прямую регрессию (положительную), возникающую при условии, если с увеличением или уменьшением значений факторного признака значения результативного признака также соответственно увеличиваются или уменьшаются;
-обратную (отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением значений факторного признака значения результативного признака соответственно уменьшаются или увеличиваются.
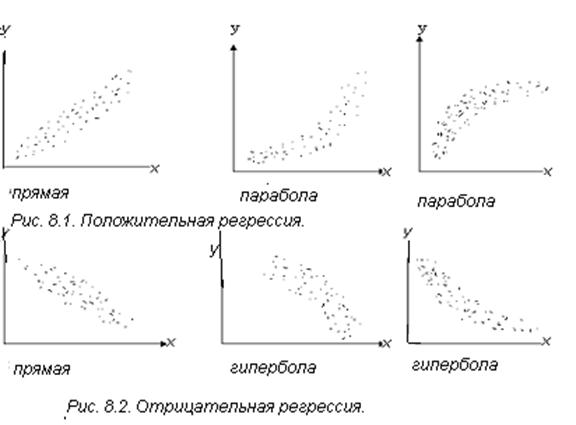
Определить тип уравнений можно, исследуя зависимость графически. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат - результативного. Каждое пересечение линий, проводимых через эти оси, обозначается точкой. При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.
Проиллюстрировать их графическое изображение можно рисунками 8.1 и 8.2.
Оценка параметров уравнений регрессии (а0,а1,а2) осуществляется методом наименьшим квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
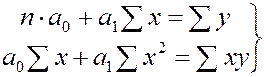 , где
, где
n- объем исследуемой совокупности (число единиц наблюдения).
В уравнениях регрессии параметр а0 показывает усередненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр а1)-коэффициент регрессии показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.Параметр а2 характеризует степень ускорения или замедления кривизны параболы и при а2›0 парабола имеет минимум, а при а2‹0 – максимум. Параметр а1 характеризует крутизну кривой, а параметр а0 вершину кривой.
Коэффициент регрессии применяют для определения коэффициента эластичности, который показывает, на сколько процентов в среднем изменяется величина результативного признака у при изменении признака-фактора х на один процент.
Коэффициент эластичности определяется по формуле 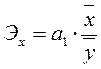 .
.
Систему нормальных уравнений для нахождения параметров гиперболы можно представить следующим образом:
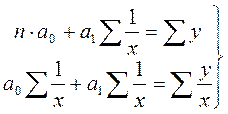
Система нормальных уравнений при параболической зависимости имеет следующий вид:
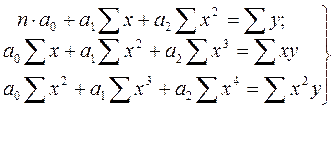
Решив соответствующие системы уравнений, и найдя значения неизвестных коэффициентов 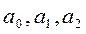 , получают уравнение регрессии. Затем определяются теоретические значения
, получают уравнение регрессии. Затем определяются теоретические значения 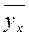 .
.
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторов.
В случае наличия между двумя признаками линейной зависимости теснота связи измеряется линейным коэффициентом корреляции.
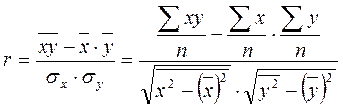
Линейный коэффициент корреляции изменяется от-1до+1: -1≤ r ≤+1.
Знаки коэффициентов регрессии и корреляции совпадают.
Значимость линейного коэффициента корреляции проверяется на основе t критерия Стьюдента: 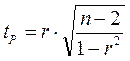 . Если расчетное значение
. Если расчетное значение
tp›tТ (табличного), то это свидетельствует о значимости линейного коэффициента корреляции.
По сгруппированным данным в случае линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют корреляционное отношение.
Эмпирическое корреляционное отношение рассчитывается по данным группировки по формуле 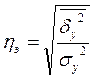 , где
, где
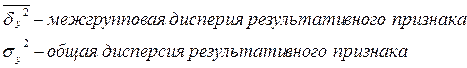
Корреляционное отношение изменяется в пределах от 0 до 1 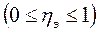
Подкоренное выражение корреляционного отношения представляет собой коэффициент детерминации( 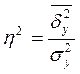 ) , который показывает долю вариации результативного признака под влиянием вариации признака-фактора.
) , который показывает долю вариации результативного признака под влиянием вариации признака-фактора.
Для оценки значимости уравнения регрессии в целом, особенно при нелинейных зависимостях, используют F-критерий Фишера.
Проверка значимости коэффициента детерминации осуществляется также по F-критерию Фишера, расчетное значение которого
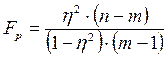 , где n-число наблюдений, а m-число признаков (при парной корреляции m=2). Вычисленные значения Fр сравнивается с критическим (табличным) FT для принятого уровня значимости и чисел степеней свободы v1=m-1 и v2=n-m. Значимость подтверждается, если Fp›FT.
, где n-число наблюдений, а m-число признаков (при парной корреляции m=2). Вычисленные значения Fр сравнивается с критическим (табличным) FT для принятого уровня значимости и чисел степеней свободы v1=m-1 и v2=n-m. Значимость подтверждается, если Fp›FT.
Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока :
ηэ 0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99
Сила связи Слабая Умеренная Заметная Тесная Весьма тесная
Глава 9.
Дата добавления: 2014-11-13; просмотров: 1018; Мы поможем в написании вашей работы!; Нарушение авторских прав |