Средние характеристики ряда динамики.

Средние характеристики ряда динамики охватывают изменение явления за весь период, к которому относится ряд динамики. К средним характеристикам относятся: средний уровень ряда, средний абсолютный прирост, средний темп роста и средний темп прироста.

Средний уровень ряда ( ) показывает, какова средняя величина уровня характерная для всего периода ряда. Средний уровень ряда исчисляется

по-разному для интервальных и моментных рядов.

Для интервального ряда с равным интервалом, он определяется по средней арифметической простой, делением суммы уровней ряда на число периодов.

, где - сумма уровней ряда, n - число периодов.

Для интервального ряда с неравным интервалом средний уровень ряда определяется по формуле средней арифметической взвешенной , где t_i - величина интервала.

Для моментного ряда с равным интервалом средний уровень ряда определяется по формуле средней хронологической .

Для моментного ряда с неравным интервалом средний уровень ряда можно определить по формуле средней скользящей взвешенной: .

В различных источниках эту среднюю называют по-разному: средняя арифметическая взвешенная моментного ряда, средняя хронологическая взвешенная, средняя скользящая взвешенная.

Средний абсолютный прирост характеризует скорость развития явления во времени. Его можно определить как среднюю величину из цепных абсолютных приростов 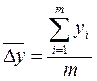, где m - число цепных абсолютных приростов. Либо по данным уровней ряда , т.к. сумма цепных абсолютных приростов всегда равна базисному абсолютному приросту. Средний темп роста дает сводную характеристику интенсивности изменения явления за весь период ряда динамики. Он может быть определен по формуле средней геометрической на основании данных о цепных коэффициентах роста.

, где m - число темпов роста. Либо на основании данных об уровнях ряда

, т.к. произведение цепных коэффициентов роста всегда равно базисному коэффициенту роста. Эта формула ценна тем, что позволяет определить средний темп роста при отсутствии нескольких или всех промежуточных данных.

Средний темп прироста определяется на основании данных о среднем темпе роста как разность: .