
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Выявление основной тенденции динамических рядов.
Одним из методов анализа и обобщения динамических рядов является выявление его основной тенденции - трэнда. В статистической практике выявление основной тенденции развития осуществляют двумя способами: сглаживания и аналитического выравнивания.
Сглаживание - это механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней;
выравнивание аналитическое - это выравнивание с применением кривой, проведенной между конкретными фактическими уровнями таким образом, чтобы она отражала тенденцию, присущую ряду, освобождая его от незначительных колебаний.
Сглаживание может осуществляться методом укрупнения интервала, т.е., например, ряд суточного выпуска продукции заменить рядом ежемесячного выпуска продукции. Таким образом, сглаживаются суточные колебания выпуска. Сглаживание методом простой скользящей средней, заключается в том, что вычисляется средний уровень из трех, пяти, семи и т.д. уровней. Таким образом, вместо каждого уровня ряда берутся средние из окружающих его уровней с обеих сторон. В этой средней сглаживаются случайные отклонения. Она будет скользящей, поскольку период осреднения все время меняется. Из него вычитается один предыдущий и прибавляется один следующий. Например, скользящая средняя из 3-х уровней будет 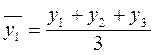 ,
,  и т.д. Средняя скользящая относится в этом случае ко 2-му, 3-му, 4-му и т.д. периоду. Если скользящая средняя находится по четному число членов, то для отнесения ее к конкретному периоду необходимо произвести центрирование, т.е. найти среднюю из двух смежных скользящих средних. Недостаток метода простой скользящей средней в том, что сглаженный ряд динамики сокращается (укорачивается) для начала и конца.
и т.д. Средняя скользящая относится в этом случае ко 2-му, 3-му, 4-му и т.д. периоду. Если скользящая средняя находится по четному число членов, то для отнесения ее к конкретному периоду необходимо произвести центрирование, т.е. найти среднюю из двух смежных скользящих средних. Недостаток метода простой скользящей средней в том, что сглаженный ряд динамики сокращается (укорачивается) для начала и конца.
Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени: y=f(t).
В практике экономических исследований применяется аналитическое выравнивание по любому рациональному многочлену.
Правильно установить тип кривой, тип аналитической зависимости от времени - является одной из трудных задач статистики. К этому следует подходить с большой осторожностью. Аналитическое выравнивание состоит в подборе для данного ряда динамики теоретической кривой, наилучшим образом описывающей эмпирические данные. Это могут быть различные функции: полиномы степени, экспоненты, логистические кривые и другие виды.
Полиномы имеют следующий вид:
полином первой степени  (прямая);
(прямая);
полином второй степени  (парабола 2-го порядка);
(парабола 2-го порядка);
полином n-ой степени  .
.
 параметры полиномов, t –условное обозначение времени. Параметр а0 трактуется как характеристика средних условий ряда динамики, параметры
параметры полиномов, t –условное обозначение времени. Параметр а0 трактуется как характеристика средних условий ряда динамики, параметры  как изменения ускорения.
как изменения ускорения.
Наиболее приближенный и простой способ определения формы теоретической кривой – графический.
После выбора вида уравнения необходимо определить параметры уравнения. Самый распространенный способ определения параметров уравнения - это метод наименьших квадратов.
Система нормальных уравнений для оценивания параметров прямой
 примет вид:{
примет вид:{ 
В статистической практике применяется упрощенный расчет параметров уравнения, который заключается в переносе начала отсчета времени в середину ряда динамики. Тогда  и система нормальных уравнений упрощается для прямой {
и система нормальных уравнений упрощается для прямой { 
Аналогично для параболы второго порядка система нормальных уравнений будет {  , а после упрощения
, а после упрощения
{  , т.к. суммы всех нечетных степеней t будут равны нулю.
, т.к. суммы всех нечетных степеней t будут равны нулю.
Решив системы относительно неизвестных параметров, получим величины параметров соответствующих уравнений. Подставляя вместо t значения времени, получим теоретические значения  , которые будут отражать тенденцию.
, которые будут отражать тенденцию.
Дата добавления: 2014-11-13; просмотров: 305; Мы поможем в написании вашей работы!; Нарушение авторских прав |