
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Индексы качественных показателей. Факторный анализ
Качественные показатели определяют уровень исследуемого итогового показателя и определяются путём соотношения итогового показателя и определённого количественного показателя (например, средняя заработная плата определяется путём соотношения фонда заработной платы и количества работников).
К индексам качественных показателей относятся индексы цен, себестоимости, средней заработной платы, производительности труда.
Самым распространенным индексом в этой группе является индекс цен.
Индивидуальный индекс цен характеризует изменение цен по одному виду продукции и определяется по формуле:
 , (3.71)
, (3.71)
где p1 и p0 - цена за единицу продукции в текущем и базисном периодах.
Соответственно определяются индексы себестоимости и затрат рабочего времени по каждому виду продукции.
Агрегатный индекс цен определяет среднее изменение цены р по совокупности определенных видов продукции q.
Для характеристики среднего изменения цен на потребительские товары используют индекс цен, предложенный Э. Ласпейресом (индекс Ласпейреса):
 , (3.72)
, (3.72)
где q0 - потребительская корзина (базовый период);
p0 и p1 - соответственно цены базисного и отчётного периодов.
Если количество набора продуктов принимается на уровне отчётного периода (q1 ), то в этом случае индекс цен именуется индексом Пааше:
 , (3.73)
, (3.73)
Если известны индивидуальные индексы цен по отдельным видам продукции и стоимость отдельных видов продукции, то применяются средние взвешенные индексы цен (средний взвешенный арифметический и средний взвешенный гармонический индексы цен).
Формула среднего взвешенного арифметического индекса цен:
 , (3.74)
, (3.74)
где i - индивидуальный индекс по каждому виду продукции;
p0q0 - стоимость продукции каждого вида в базисном периоде.
Формула среднего взвешенного гармонического индекса цен:
 , (3.75)
, (3.75)
где p1 q1 - стоимость продукции каждого вида в текущем периоде.
В статистической практике очень широко используется агрегатный территориальный индекс цен, который может быть рассчитан по следующей формуле:
 , (3.76)
, (3.76)
где pA pB - цена за единицу продукции каждого вида соответственно на территории А и В;
qA - количество выработанной или реализованной продукции каждого вида по территории А (в натуральном выражении).
Из формулы видно, что в данном индексе в качестве фиксированного показателя (веса) принят объём продукции территории А. При расчёте данного индекса в качестве веса можно принять также объём продукции территории В или суммарный объём продукции двух территорий.
Возможны два способа расчёта индексов: цепной и базисный.
Цепные индексы получают путём сопоставления текущих уровней с предшествующим, при этом база сравнения постоянно меняется.
Базисные индексы получают путём сопоставления с тем уровнем периода, который был принят за базу сравнения.
В качестве примера можно привести цепные и базисные индексы цен.
Цепные индивидуальные индексы цен имеют следующий ряд расчёта:
 ,
,  ,
,  и т.д. (3.77)
и т.д. (3.77)
Базисные индивидуальные индексы цен:


 , и т.д. (3.78)
, и т.д. (3.78)
Следует помнить, что произведение цепных индивидуальных индексов цен равно последнему базисному индексу.
Цепные агрегатные индексы цен:


 и т.д. (3.79)
и т.д. (3.79)
Базисные агрегатные индексы цен:

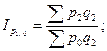
 и т.д. (3.80)
и т.д. (3.80)
Между индексами существует также взаимосвязь и взаимозависимость, как и между самими экономическими явлениями, что позволяет проводить факторный анализ. Благодаря индексному методу можно рассматривать все факторы независимо друг от друга, что даёт возможность определить размер абсолютного изменения сложного явления за счёт каждого фактора в отдельности.
Для выявления роли каждого фактора в отдельности индекс сложного показателя разлагают на частные (факторные) индексы, которые характеризуют роль каждого фактора. При этом используют два метода:
1) метод обособленного изучения факторов;
2) последовательно-цепной метод.
При первом методе сложный показатель берётся с учётом изменения лишь того фактора, который взят в качестве исследуемого, все остальные остаются неизменными на уровне базисного периода.
Последовательно-цепной метод предполагает использование системы взаимосвязанных индексов, которая требует определённого расположения факторов. Как правило, на первом месте в цепи располагают качественный фактор.
При определении влияния первого фактора все остальные сохраняются в числителе и знаменателе на уровне базисного периода, при определении второго факторного индекса первый фактор сохраняется на уровне базисного периода, а третий и все последующие - на уровне отчётного периода, при определении третьего факторного индекса первый и второй факторы сохраняются на уровне базисного периода, четвёртый и все остальные - на уровне отчётного периода и т.д.
Дата добавления: 2014-11-13; просмотров: 246; Мы поможем в написании вашей работы!; Нарушение авторских прав |