Корреляционно-регрессионный метод анализа

Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными).

Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х.

Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у.

Важнейшей задачей является определение формы связи с последующим расчётом параметров уравнения, или, иначе, нахождение уравнения связи (уравнения регрессии).

Могут иметь место различные формы связи:

- прямолинейная

, (3.86)

Параметр 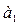называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина, результативного признака у при отклонении величины факторного признака х на одну единицу.

криволинейная в виде:

- параболы второго порядка (или высших порядков):

, (3.87)

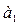Параметр характеризует степень ускорения или замедления кривизны параболы и при > 0 парабола имеет минимум, а при < 0 – максимум. Параметр характеризует кривизну кривой, а параметр - вершину кривой.

- гиперболы:

, (3.88)

и т.д.

Точное аналитическое выражение имеет только функциональная связь. Корреляционная связь может быть выражена лишь приближённо, при наличии определённых условий.

Параметры для всех этих уравнений связи, как правило, определяют из системы нормальных уравнений, которые должны отвечать требованию метода наименьших квадратов (МНК), чтобы :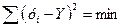

, (3.89)

Если связь выражена параболой второго порядка ( ), то систему нормальных уравнений для отыскания параметров a₀ , a₁ , a₂ (такую связь называют множественной, поскольку она предполагает зависимость более чем двух факторов) можно представить в виде системы:

, (3.90)

Рассмотрим применение приёмов корреляционного анализа на конкретном примере.

Анализ данных табл. 3.4 показывает, что с увеличением стоимости основных фондов растёт, как правило, и выпуск продукции. Однако, мы не можем утверждать, что увеличение стоимости основных фондов, например, на 1 млн. руб. , приводит к фактическому увеличению выпуска продукции на определённую сумму.

Таблица 3.4