
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непараметрические показатели связи
В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые непараметрические методы.
Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет её рангом. Если значения признака совпадают, то определяется средний ранг путём деления суммы рангов на число значений.
Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены К. Спирменом и М. Кендэлом.
Коэффициент корреляции рангов Спирмена (р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле:
 , (3.96)
, (3.96)
где 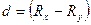 , т.е. разность рангов каждой пары значений х и у,
, т.е. разность рангов каждой пары значений х и у,
п – число наблюдений.
Коэффициент колеблется от -1 до +1. Если ранги по обоим признакам совпадают, то ∑d² = 0, р = 1 и, следовательно, связь полная прямая. Если р = - 1, связь полная обратная, при р = 0 связь между признаками отсутствует.
Значимость коэффициента Спирмена проверяется на основе t критерия Стьюдента по формуле:
 , (3.97)
, (3.97)
Значение коэффициента считается существенным, если 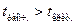 (
(  ).
).
Ранговый коэффициент корреляции Кендалла (  ) можно определить по формуле:
) можно определить по формуле:
 , (3.98)
, (3.98)
где S = P + Q.
Этот коэффициент измеряется в интервале от -1 до 1 и интерпретируется так же, как и коэффициент Пирсона, но он даёт более строгую оценку связи, чем коэффициент Спирмена  . Это соотношение выполняется при брльшом числе наблюдений, n>30. и слабых, либо умеренно тесных связях.
. Это соотношение выполняется при брльшом числе наблюдений, n>30. и слабых, либо умеренно тесных связях.
К непараметрическим методам исследования можно отнести коэффициент ассоциации Кас и коэффициент контингенции Ккон , которые используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков.
Для определения этих коэффициентов создается расчётная таблица (таблица «четырех полей»), где статистическое сказуемое схематически представлено в следующем виде:
| Признаки | А (да) | А (нет) | Итого |
| В (да) | а | b | a + b |
| В (нет) | с | d | c + d |
| Итого | а + с | b + d | n |
Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков  ; n - общая сумма частот.
; n - общая сумма частот.
Коэффициент ассоциации можно рассчитать по формуле:
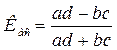 ,(3.99)
,(3.99)
Коэффициент контингенции рассчитывается по формуле:
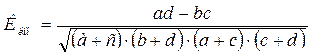 ,(4.0)
,(4.0)
Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации.
Связь считается подтверждённой, если 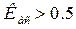 или
или 
Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (КП ) и Чупрова (  ).
).
Для исследования такого рода связи первичную статистическую информацию располагают в форме таблицы:
| Признаки | А | В | С | Итого |
| D | m11 | m12 | m13 | ∑m1j |
| E | m21 | m22 | m23 | ∑m2j |
| F | m31 | m32 | m33 | ∑m3j |
| Итого | ∑mj1 | ∑mj2 | ∑mj3 | П |
Здесь mij - частоты взаимного сочетания двух атрибутивных признаков; П - число пар наблюдений.
Коэффициент взаимной сопряженности Пирсона определяется по формуле:
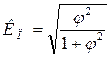 , (4.1)
, (4.1)
Коэффициент Чупрова определяется по формуле:
 , (4.2)
, (4.2)
где  - показатель средней квадратической сопряженности, определяемый путём вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки:
- показатель средней квадратической сопряженности, определяемый путём вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки:
 -1
-1
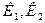 - число групп по каждому из признаков.
- число групп по каждому из признаков.
Величина коэффициента взаимной сопряженности, отражающая тесноту связи между качественными признаками, колеблется в пределах от 0 до 1.
Коэффициент Фехнера характеризует элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объём исходной информации. Данный коэффициент определяется по формуле:
 , (4.3)
, (4.3)
где na - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической;
nb - соответственно количество несовпадений.
Коэффициент Фехнера может изменяться в пределах -1,0 до +1,0. при значении равном 1 он указывает на полную прямую связь, при значении -1 на полную обратную связь, при нулевом значении – на отсутствие связи.
Например, имеются данные о выпуске продукции (х) на 6 однотипных предприятиях и потреблении на них электроэнергии (у):
| Выпуск продукции | ||||||
| Потребление электричества |
Рассчитаем средние значения для х и у


| Выпуск продукции | ||||||
| Потребление электричества | ||||||

| - 6 | - 4 | -1 | |||

| - 9,83 | - 4,83 | - 0,83 | - 2,83 | 3,17 | 15,17 |
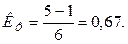
Судя по полученному значению коэффициента, связь можно считать достаточно сильной.
Недостаток показателя Фехнера состоит в том, что разные по абсолютной величине отклонения имеют одинаковый вес. Более совершенным показателем степени тесноты связи является линейный коэффициент корреляции.
Вопросы для самоконтроля
1. В чём состоит отличие между функциональной и корреляционной связью?
2. В чём заключается сущность корреляционно связи?
3. Какие основные задачи решают с помощью корреляционного и регрессионного анализа?
4. Какими показателями измеряется теснота корреляционной связи?
5. В чём состоит значение уравнения регрессии? Что характеризуют коэффициенты регрессии?
6. Какие непараматрические методы применяют для моделирования связи?
Дата добавления: 2014-11-13; просмотров: 480; Мы поможем в написании вашей работы!; Нарушение авторских прав |