Теорема об изменении количества движения материальной точки

(Фрагменты математической симфонии)

Связь импульса силы с основным уравнением ньютоновской динамики выражает теорема об изменении количества движения материальной точки.

Теорема. Изменение количества движения материальной точки за некоторый промежуток времени равно импульсу силы ( ), действующей на материальную точку за тот же промежуток времени.Математическое доказательство этой теоремы можно назвать фрагментом математической симфонии. Вот он.

(128)

Дифференциал количества движения материальной точки равен элементарному импульсу 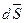силы, действующей на материальную точку. Интегрируя выражение (128) дифференциала количества движения материальной точки, имеем

(129)

Теорема доказана и математики считают свою миссию законченной, а у инженеров, судьба которых - свято верить математикам, возникают вопросы при использовании доказанного уравнения (129). Но их прочно блокирует последовательность и красота математических действий (128 и 129), которые завораживают и побуждают назвать их фрагментом математической симфонии. Сколько поколений инженеров соглашались с математиками и трепетали перед таинственностью их математических символов! Но вот нашёлся инженер, несогласный с математиками, и задаёт им вопросы.

Уважаемые математики! Почему ни в одном из Ваших учебников по теоретической механике не рассматривается процесс применения Вашего симфонического результата (129) на практике, например, при описании процесса разгона автомобиля? Левая часть уравнения (129) предельно понятна. Автомобиль начинает разгон со скорости и завершает его, например, на скорости . Вполне естественно, что уравнение (129) становится таким

(130)

И сразу возникает первый вопрос: как же из уравнения (130) определить силу , под действием которой автомобиль разогнан до скорости 10м/с? Ответа на этот вопрос нет ни в одном из неисчислимых учебников по теоретической механике. Пойдём дальше. После разгона автомобиль начинает равномерное движение с достигнутой скоростью 10м/с. Какая же сила движет автомобиль????????? У меня ничего не остаётся, как краснеть вместе с математиками. Первый закон ньютоновской динамики утверждает, что при равномерном движении автомобиля на него не действуют никакие силы, а автомобиль, образно говоря, чихает на этот закон, расходует бензин и совершает работу, перемещаясь, например, на расстояние 100 км. А где же сила, совершившая работу по перемещению автомобиля на 100км? Симфоническое математическое уравнение (130) молчит, а жизнь продолжается и требует ответа. Начинаем искать его.

Поскольку автомобиль движется прямолинейно и равномерно, то сила, перемещающая его, постоянна по величине и направлению и уравнение (130) становится таким

(131)

Итак, уравнение (131) в данном случае описывает ускоренное движение тела. Чему же равна сила ? Как выразить её изменение с течением времени? Математики предпочитают обходить этот вопрос и оставляют его инженерам, полагая, что они должны искать ответ на этот вопрос. У инженеров остаётся одна возможность – учесть, что если после завершения ускоренного движения тела, наступает фаза равномерного движения, которое сопровождается под действием постоянной силы представить уравнение (131) для момента перехода от ускоренного к равномерному движению в таком виде

(132)

Стрелка в этом уравнении означает не результат интегрирования этого уравнения, а процесс перехода от его интегрального вида к упрощённому виду. Сила в этом уравнении эквивалентна усреднённой силе, изменившей количество движения тела от нуля до конечного значения . Итак, уважаемые, математики и физики-теоретики, отсутствие Вашей методики определения величины Вашего импульса вынуждает нас упрощать процедуру определения силы , а отсутствие методики определения времени действия этой силы вообще ставит нас в безвыходное положение и мы вынуждены использовать выражение 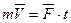для анализа процесса изменения количества движения тела. В результате получается, чем дольше будет действовать сила , тем больше её импульс . Это явно противоречит давно сложившимся представлениям о том, что импульс силы тем больше, чем меньше время его действия.

Обратим внимание на то, что изменение количества движения материальной точки (импульса силы) при ускоренном её движении происходит под действием ньютоновской силы и сил сопротивления движению, в виде сил, формируемых механическими сопротивлениями, и силой инерции. Но ньютоновская динамика в абсолютном большинстве задач игнорирует силу инерции, а Механодинамика утверждает, что изменение количества движения тела при его ускоренном движении происходит за счёт превышения величины ньютоновской силы над силами сопротивления движению, в том числе и над силой инерции.

При замедленном движении тела, например, автомобиля с выключенной передачей, ньютоновская сила отсутствует, и изменение количества движения автомобиля происходит за счёт превышения сил сопротивления движению над силой инерции, которая движет автомобиль при его замедленном движении [1].

Как же теперь вернуть результаты отмеченных «симфонических» математических действий (128) в русло причинно-следственных связей? Выход один – найти новое определение понятиям «импульс силы» и «ударная сила». Для этого разделим обе части уравнения (132) на время t. В результате будем иметь

. (133)

Обратим внимание на то, что выражение mV/t - скорость изменения количества движения (mV/t) материальной точки или тела. Если учесть, что V/t – ускорение, то mV/t - сила, изменяющая количество движения тела. Одинаковая размерность слева и с права знака равенства даёт нам право назвать силу F ударной силой и обозначить её символом , а импульс S - ударным импульсом и обозначить его символом 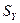. Из этого следует и новое определение ударной силы. Ударная сила , действующая на материальную точку или тело, равна отношению изменения количества движения материальной точки или тела ко времени этого изменения.

. (134)

Обратим особое внимание на то, что в формировании ударного импульса 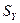(134) участвует только ньютоновская сила, которая изменила скорость автомобиля от нулевого значения до максимального - , поэтому уравнение (134) всецело принадлежит ньютоновской динамике. Поскольку величину скорости фиксировать экспериментально значительно легче, чем - ускорения, то формула (134) очень удобна для расчётов.

Из уравнения (134) следует такой необычный результат.

. (135)

Обратим внимание на то, что согласно новым законам механодинамики генератором импульса силы при ускоренном движении материальной точки или тела является ньютоновская сила [1]. Она формирует ускорение движения точки или тела, при котором автоматически возникает сила инерции, направленная противоположно ньютоновской силе и ударная ньютоновская сила должна преодолевать действие силы инерции, поэтому сила инерции должна быть представлена в балансе сил в левой части уравнения (134). Так как сила инерции равна массе точки или тела, умноженной на замедление , которое она формирует, то уравнение (134) становится таким

(136)

Уважаемые математики! Видите, какой вид приняла математическая модель, описывающая ударный импульс, который ускоряет движение ударяемого тела от нулевой скорости до максимальной V (11). Теперь проверим её работу в определении ударного импульса , который равен ударной силе , выстрелившей 2-й энергоблок СШГ (рис. 120), а Вам оставим Ваше бесполезное уравнение (132). Чтобы не усложнять изложение, мы оставим пока формулу (134) в покое и воспользуемся формулами, дающими усреднённые значения сил. Видите, в какое положение Вы ставите инженера, стремящегося решить конкретную задачу.

Начнём с динамики Ньютона. Эксперты установили, что 2-й энергоблок поднялся на высоту 14м. Поскольку он поднимался в поле силы тяжести, то на высоте h=14м его потенциальная энергия оказалась равной

, (137)

а средняя кинетическая энергия была равна

(138)

Рис. 120. Фото машинного зала до катастрофы [53]

Из равенства кинетической (138) и потенциальной (137) энергий следует средняя скорость подъёма энергоблока (рис. 121, 122)

. (139)

Рис. 121. Фотон машинного зала после катастрофы [53]

Согласно новым законам механодинамики подъём энергоблока состоял из двух фаз (рис. 123): первая фаза ОА - ускоренный подъём и вторая фаза АВ – замедленный подъём [1], [53], [54].

Время и расстояния их действия, примерно, равны ( 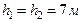). Тогда кинематическое уравнение ускоренной фазы подъёма энергоблока запишется так

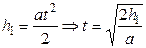. (140)

Рис. 122. Вид колодца энергоблока и самого энергоблока после катастрофы [53]

Закон изменения скорости подъёма энергоблока в первой фазе имеет вид

. (141)

Рис. 123. Закономерность изменения скорости V полёта энергоблока

Подставляя время из уравнения (140) в уравнение (141), имеем

. (142)

Время подъёма блока в первой фазе определится из формулы (140)

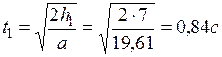. (143)

Тогда общее время подъёма энергоблока на высоту 14м будет равно . Масса энергоблока и крышки равна 2580 тонн. Согласно динамике Ньютона сила , поднимавшая энергоблок, равна

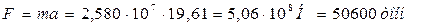. (144)

Уважаемые математики! Следуем Вашим симфоническим математическим результатам и записываем Вашу формулу (129), следующую из динамики Ньютона, для определения ударного импульса, выстрелившего 2-й энергоблок

(145)

и задаём элементарный вопрос: как определить время действия ударного импульса, выстрелившего 2-й энергоблок????????????

Уважаемые!!! Вспомните, сколько мела исписали на учебных досках поколения Ваших коллег, заумно уча студентов, как определять ударный импульс и никто не пояснил, как определять время действия ударного импульса в каждом конкретном случае. Вы скажете время действия ударного импульса равно интервалу времени изменения скорости энергоблока от нуля до, будем считать, максимального значения 16,75 м/с (139). Оно в формуле (143) и равно 0,84 с. Соглашаемся пока с Вами и определяем усреднённую величину ударного импульса

. (146)

Сразу возникает вопрос: а почему величина ударного импульса (146) меньше ньютоновской силы 50600тонн? Ответа, у Вас, уважаемые математики, нет [55]. Пойдём дальше.

Согласно динамике Ньютона, главная сила, которая сопротивлялась подъёму энергоблока, - сила тяжести . Так как эта сила направлена против движения энергоблока, то она генерирует замедление, которое равно ускорению свободного падения . Тогда сила гравитации, действующая на летящий вверх энергоблок, равна

. (147)

Других сил, препятствовавших действию ньютоновской силы 50600 тонн (144), динамика Ньютона не учитывает, а механодинамика утверждает, что подъёму энергоблока сопротивлялась и сила инерции, равная [55]

. (148)

Сразу возникает вопрос: как найти величину замедления движению энергоблока? Динамика Ньютона молчит, а механодинамика отвечает: в момент действия ньютоновской силы, поднимавшей энергоблок, ей сопротивлялись: сила тяжести и сила инерции, поэтому уравнение сил, действовавших на энергоблок в этот момент, записывается так [55]:

. (149)

Отсюда находим замедление

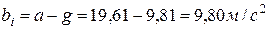. (150)

Величина, силы инерции, замедлявшей движение энергоблока в первой фазе его движения, будет равна

. (151)

Итак, сумма сил, сопротивлявшихся действию ньютоновской силы, равна самой ньютоновской силе (144)

. (152)

Не удивляйтесь, этот результат – следствие нового главного принципа механодинамики, который Вы ещё не знаете. Он заменил аналогичный, давно используемый, ошибочный принцип Даламбера. Красивый баланс (152), но в нём нет сил сопротивления разрыву 80 шпилек, которые крепили крышку энергоблока (рис. 124).