Расчет источника гармонических колебаний

Пример 1. Рассчитать источник гармонических колебаний (см. п. 1.1) по схеме рис. 2, если заданы следующие исходные данные: i_J1 = sin(10³ t + 270°) A, e₂ = 600 sin(10³ t + 225°) B, E₃ = 500 + j500 B, R₁ = 30 Ом, C₂ = 20/3 мкФ, R₃ = 150 Ом, L₃ = 100 мГн, R₄ = 100 Ом, C₅ = 10 мкФ, L₆ = 100 мГн, R₇ = 20 Ом.

Решение. Предварительная подготовка схемы к расчету заключается в выборе положительных направлений токов в ветвях и их обозначении. Кроме того, необходимо обозначить все узлы схемы буквенными или цифровыми индексами. Для перехода к комплексной схеме замещения (рис. 3) все независимые источники нужно представить в комплексной форме (в виде комплексных амплитуд или комплексных действующих значений) и рассчитать комплексные сопротивления всех ветвей схемы. Так, комплексные действующие значения источников будут равны:
i_J1 J₁ = 4exp( j270°) = – j4, e₂ E₂ = exp ( j225°) = –300
– j300, а комплексные сопротивления при w = 10³ c^–1: Z₁ = R₁ = 30, Z₂ = –jX_C2 = –j/(wC₂) = –j150, Z₃ = R₃ + jX_L3 = R₃ + jwL₃ = 150 + j100, Z₄ = R₄ = 100, Z₅ = –jX_C5 = –j/(wC₅) = –j100, Z₆ = jX_L6 = jwL₆ = j100, Z₇ = R₇ = 20, где — символ соответствия между оригиналом и изображением функции.

Рис. 3 Рис. 4

Для упрощения расчета схемы применим эквивалентное структурное преобразование пассивного треугольника Z₄–Z₅–Z₆ в звезду, обозначая ее сопротивления, например, следующим образом: Z₄₅ = Z₄Z₅/(Z₄ + Z₅ + Z₆) = 100(–j100)/(100 – j100 + j100) = –j100, Z₄₆ = Z₄Z₆ /(Z₄ + Z₅ + Z₆) = 100 j100/100 = j100, Z₅₆ = Z₅Z₆/(Z₄ + Z₅ + Z₆) =100.

Эквивалентная схема после преобразования имеет два элементарных контура и два узла (рис. 4). Также в схеме существует ветвь с идеальным источником тока. Для определения токов воспользуемся методом контурных токов (МКТ). Число независимых уравнений, составленных по МКТ, равно числу независимых контуров. Через ветвь с источником тока должен протекать лишь один и только один контурный ток, равный с учетом выбранного направления току источника тока. Поэтому число независимых уравнений равно 1. Это уравнение должно быть составлено относительно неизвестного контурного тока I₁₁. В канонической форме при выбранных I₁₁ и I₂₂ = J₁= –j4 (см. рис. 4) оно имеет вид I₁₁Z₁₁ + I₂₂Z₁₂ = E₁₁, где собственное сопротивление первого контура Z₁₁ = Z₂ + Z₃+ Z₄₅ + Z₄₆ = –j150 + 150 + j100 – j100 + j100 = 150 – j50, а общее сопротивление ветви, принадлежащей первому и второму контурам, Z₁₂ = +(Z₂ + Z₄₆) = –j150 + j100 = –j50. Знак «плюс» сопротивления Z₁₂ обусловлен одинаковым направлением контурных токов I₁₁ и I₂₂ в смежной ветви Z₂ – Z₄₆ – E₂. Контурная ЭДС E₁₁ = E₂ + E₃ = –300 – j300 +500 + j500 = 200 +
+ j200. Из уравнения I₁₁(150 – j50) + (–j4)(–j50) = 200 + j200 находим I₁₁ = 2 + j2. Комплексное значение тока указанного направления в ветви схемы (см. рис. 4) равно алгебраической сумме комплексных значений контурных токов, протекающих по этой ветви: I₃ = I₁₁ = 2 + j2, I₂ = I₁₁ + I₂₂ = (2 + j2) + (–j4) = 2 – j2. В обоих случаях контурные токи входят в уравнение со знаком «плюс», так как их направления совпадают с направлением искомого тока ветви.

Определяем токи I_4, I_5, и I₆ в пассивном треугольнике по известным из расчета токам в эквивалентной звезде. При этом учитываем, что напряжения треугольника и эквивалентной звезды равны. Из схемы рис. 3 следует, что I₄ = U_db /Z₄, I₅ = U_cb /Z₅, I₆ =
= U_dc/Z₆. Из схемы рис. 4: U_db = – I₃Z₄₅ – I₂Z₄₆ = – 400, U_cb = I₁Z₅₆ –
– I₃Z₄₅ = –200 – j200, U_dc = – I₁Z₅₆ – I₂Z₄₆ = – 200 + j200. Следовательно, I₄ = –400/100 = –4, I₅ = (–200 – j200)/j100 = 2 – j2, I₆ = (–200
+ j200)/j100 = 2 + j2.

Проверим выполнение первого закона Кирхгофа для узлов схемы рис. 3. Узел b: I₄ + I₃ + I₅ = (– 4) + (2 + j2) + (2 – j2) = 0, узел с: – I₅ + I₆ + I₁ = – (2 – j2) + (2 + j2) + (– j4) = 0, узел d: – I₂ – I₄ – I₆ = – (2 – j2) – (–j4) – (2 + j2) = 0.

Амперметр, включенный в ветвь с E₂ (см. рис. 2), измеряет действующее значение тока I₂: I₂ = |I₂| = = = 2,82A.

Для определения показания вольтметра V, включенного между точками а и q схемы рис. 3, предварительно рассчитаем комплексное действующее значение напряжения, выбрав произвольно его направление, например U_aq. Из уравнения – I₂Z₂ + I₆Z₆ – I₁Z₇ – U_aq = –­E₂, составленного по второму закону Кирхгофа для контура a–d–c–q, находим: U_aq= –200 + j280. Вольтметр, измеряющий действующее значение напряжения U_aq, покажет U_aq =
= = 344 В.

Определим напряжение на зажимах источника тока, выбрав его направление, например U_fa (см. рис. 3). Уравнение, составленное согласно второму закону Кирхгофа, может быть записано для любого контура, в который входит ветвь с источником тока. При обходе контура a–d–c–q–f по ходу часовой стрелки получим уравнение –I₂Z₂ + I₆Z₆ – I₁(Z₁ + Z₇) + U_fa = –E₂, откуда U_fa = 200 – j400. Баланс мощностей составляем для исходной схемы (см. рис. 3). Полная комплексная мощность источников должна быть равна полной комплексной мощности потребителей:

где I_k —действующее значение тока в k-й ветви; Z_k — комплексное сопротивление ветви; I ^* — сопряженный комплекс I.

Для данной схемы при указанных направлениях источников, выбранных направлений токов в ветвях и напряжении U_fa на источнике тока имеем: å S_и = E₂ I^*₂ + E₃ I ^*₃ + U_fa J ^*₁ = (–300 – j300) ´ (2 + j2) + (500 +j500)(2 – j2) + (200 – j400)( j4) = 3600 – j400; åS_п= I ²₁(Z₁ + Z₇) +I ²₂ Z₂ + I ²₃ Z₃ + I ²₄ Z₄ + I ²₅ Z₅ + I ²₆ Z₆ = 16
´ (30 +20) + 8(–j150) + 8(150 +j100) + 16 (100) + 8(–j100) +
+ 8( j100) = 3600 – j400. Таким образом, баланс мощностей сходится, а значит, расчет проведен верно.

Запишем мгновенные значения тока i₃ и напряжения u_L3(t) на индуктивности L₃, представляющей собой первичную обмотку трансформатора. Комплексной амплитуде тока I_3m = (2 + j2) =
= 4 exp( j45°) соответствует мгновенное значение тока i(t) =
= 4 sin(10³t + 45°). Комплексному действующему значению напряжения U_L3 = I₃ jX_L3 = (2 + j2)( j100) = –200 + j200 = 200 ´
´ exp( j45°) соответствует мгновенное значение напряжения u_L3(t) = 400sin(10³t + 135^°). Кривые мгновенных значений токов i(t) или i(wt), напряжений u(t) или u(wt), построенные в декартовой системе координат (рис. 5), называются волновыми или временными диаграммами.

Рис. 5

Определим значения взаимных индуктивностей М₃₈ и М₃₉, необходимых для получения на вторичных обмотках линейного трансформатора заданных значений U₁ и U₂ (см. рис. 2). Пусть требуется получить напряжения U₁ = 5 B, U₂ = 10 B. Так как U₁ =
= X_m38 I₃ = w M₃₈ I₃, а I₃ = 2 , то M₃₈ = U₁ /(wI₃) = 5/(10³ 2 ) =
= 1,25 = 1,77 мГн. При рассчитанном значении взаимной индуктивности комплексное значение напряжения на входных зажимах повторителя напряжения U₁ = jwM₃₈ I₃ = j10³ ´ 1,25 10^–3 ´ (2 + j2) = 5exp ( j135°). (Для проверки правильности записи равенства для U₁ необходимо задаться направлением тока I₈ в L₈, записать уравнение для U₁ с учетом магнитных связей, а затем принять I₈ = 0, так как ОУ считается идеальным). Мгновенное значение напряжения u₁ = 5 sin (10³t + j135°). Заданный коэффициент связи позволяет определить значение индуктивности L₈ вторичной обмотки трансформатора. Так как k₃₈ = M₃₈ / , то, например, при k₃₈ = 0,5 L₈ = M ²₃₈ / / (k ²₃₈ L₃) = (1,25 ×10^–3)² / (0,5²×100×10^–3) = 0,125 мГн. Аналогично: M₃₉ = U₂ / (wI₃) = 10 / (10³×2 ) = 2,5 = 2,54 мГн, при k₃₉ = 0,5 L₉ = M ²₃₉ / (k ²₃₉L₃) = (2,5 ×10^–3)² / (0,5²×100×10^–3) = 0,5 мГн, U₂ = – jwM₃₉ I₃ = – j10³ ´ 2,5 ×10^–3(2 + j2) = 10 exp(–j45°) u₂ = 10 sin (10³t – j45°). Напряжение u₂ на индуктивности L₉ находится в противофазе с напряжением u₁ на L₈ (см. схему включения обмоток ТР на рис. 2).

Пример 2. Рассчитать ток I₃ в первичной обмотке трансформатора (см. рис. 2) методом эквивалентного источника.

Рис. 6

Данный метод расчета основан на теореме об эквивалентном источнике (источнике напряжения или тока) [1–4]. В соответствии с этой теоремой ток в любой ветви m–n сколь угодно сложной электрической цепи (рис. 6, а) не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником энергии, который может быть представлен последовательной (источником напряжения — рис.

6, б) или параллельной (источником тока — рис. 6, в) схемой замещения.

ЭДС идеального источника напряжения в последовательной схеме замещения должна быть равна напряжению на разомкнутых зажимах m–n схемы; ток идеального источника тока в параллельной схеме замещения равен току, протекающему между зажимами m–n, замкнутыми накоротко; внутреннее сопротивление и внутренняя проводимость эквивалентного источника должны быть равны соответственно входному сопротивлению и входной проводимости пассивной электрической цепи (источники замещены их внутренним сопротивлением) со стороны разомкнутых зажимов m–n. Эта теорема лежит в основе метода эквивалентного источника.

Решение. Расчет неизвестного тока I₃ для исходной схемы (см. рис. 3) выполним методом, например, эквивалентного источника напряжения. Найдем параметры E _ЭГ и Z _вн, учитывая, что обмотка трансформатора с индуктивностью L₃ =100 мГн включена между точками а–е.

А. Схема для определения E_ЭГ показана на рис. 7. Направление напряжения U_{ae xx}совпадает с направлением неизвестного тока I₃. Из уравнения, составленного по методу контурных токов, I₁₁(Z ₄ + Z ₅ + Z ₆) – I ₂₂ Z ₆ = 0 при условии, что I ₂₂ = J ₁ = –j4, определяем токи I₁₁ = 4, I¢₄ = I ₁₁ = 4, I¢₂ = I ₂₂ = –j4. Теперь из уравнения U_{ae xx} + I¢₄ Z₄ + I¢₂ Z₂ = E ₂ + E ₃, составленного согласно второму закону Кирхгофа для правого контура, находим E_ЭГ = U_{ae xx}= 400 + j400.

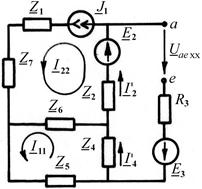
Рис. 7 Рис. 8

Б. Схема для определения внутреннего сопротивления генератора Z _вн = Z _{ае вх} показана на рис. 8 - здесь источники замещены их внутренним сопротивлением: Z _вн = R₃ + R₂ + Z ₄ (Z ₅ + Z ₆) /
/ (Z ₄ + Z ₅ + Z ₆) = 150 – j150.

На основании метода эквивалентного источника напряжения определяем: I ₃ = E _ЭГ/(Z _вн + Z_L3) = (400 + j200)/(150 – j150 + j100)
= 2 + j2, что соответствует ранее рассчитанному значению тока.