КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет электрической цепи в квазиустановившемся режиме
Пример 8. Для схемы четырехполюсника (рис. 17) рассчитать в квазиустановившемся режиме работы закон изменения напряжения на выходе четырехполюсника, если на входе действует последовательность разнополярных импульсов (рис. 18, а).
Рис.17
Решение. При квазиустановившемся режиме наблюдается установившийся переходный процесс, т.е. периодический процесс, обладающий для всех t свойствами периодичности f (t) =
= f (t + T ).
Полярность входного напряжения изменяется в точках t =
= nT/2, где n = 1, 2, 3 ... Назовем момент каждого изменения полярности напряжения моментом коммутации. В течение периода происходят две коммутации, поэтому переходный процесс разбивается на два временных интервала: первый — [0+; T/2–], второй — [T/2+; T–]. Так как процесс повторяется через период, то момент времени [nT–] соответствует [0–], а [(n + 1)T+] — [T+].
Решение системы дифференциальных уравнений внутри каждого интервала содержит некоторое число неизвестных постоянных интегрирования. Эти постоянные интегрирования определяются путем сопряжения («припасовывания») решений на границах смежных интервалов с учетом начальных условий. Решения для токов в индуктивных элементах и напряжении на конденсаторах схемы «сшиваются» на границах интервалов без разрывов, согласно законам коммутации. Решения для других напряжений, токов и их производных, которые могут иметь разрывы в момент коммутации, «сшиваются» на границах интервалов с учетом их изменения в момент коммутации.
Составим систему уравнений состояния схемы:
u1(t) = R1i1(t) ++ uC(t) + uL(t),
0 = uC (t) + R1i1(t) – R2i2(t), i0(t) = i1(t) + i2(t), (3)
где R2 = R¢2 + R²2. Система уравнений (3) в общем виде справедлива на интервале времени от 0 до ¥. Так как в моменты коммутации t = nT/2 структура схемы и значения ее параметров не изменяются, то характер переходного процесса, определяемый корнями характеристического уравнения, остается неизменным на всем интервале переходного процесса. Изменение значения u1(t) приводит к изменению значений постоянных интегрирования в выражениях для токов и напряжений. Например, если корни действительные, отрицательные и различные, то решение в общем виде для любого тока или напряжения в заданной схеме должно быть записано так:
на первом интервале yk1 = A1exp( p1t) + A2exp( p2t) + yk1вын; (4)
на втором yk2 = В1exp[ p1(t – T/2)] + В2exp[ p2(t – T/2)] + yk2вын. (5)
Второй индекс в обозначении yk указывает на его принадлежность к интервалу.
Определим изменения токов и напряжений на границе первой коммутации tk = 0. Следует помнить, что все токи и напряжения перед временем коммутации tk обозначаются y(tk–), а сразу после коммутации — y(tk+).На основании законов коммутации uC1(0+) =
= uC2(T–); i01(0+) = i02(T–) и, следовательно, DuC1 = uC1(0+) – uC2(T–) = 0; Di01 = i01(0+) – i02(T–) = 0. Вычтем из уравнений системы (3) для
t = 0+ уравнения системы для t = T– и получим разности токов и напряжений, характеризующие их изменения:
Обозначим полученные разности: uL1(0+) – uL2(T–) = DuL1; i11(0+) –
– i12(T–) = Di11; i21(0+) – i22(T–) = Di21.
Запишем систему уравнений в разностях для первой коммутации: 2U =DuL1 + R1Di11; 0 = R1Di11 – R2Di21; 0 = Di11 + Di21. Из нее определим разности токов и напряжений — зависимые начальные значения разностей токов и напряжений при первой коммутации:
i11 = 0; i21 =0; 
uL1 = 2U. (6)
Найдем таким же образом изменение токов и напряжений на границе второй коммутации t = T/2, помня, что uC2 = 0 и i02 = 0:
Обозначим разности: uL2(T/2+) – uL1(T/2–) = DuL2; i12(T/2+) –
– i11(T/2–) = Di12; i22(T/2+) – i21(T/2–) = Di22.
Запишем систему уравнений для второй коммутации в разностях: –2U = DuL2 + R1Di12, 0 = R1Di12 – R2Di22, 0 =Di12 + Di22. Отсюда найдем зависимые начальные значения разностей токов и напряжений при второй коммутации:
Di12 = 0, i22 = 0, DuL2 = –2U. (7)
Полученные разности позволяют определить постоянные интегрирования для тока в индуктивности и напряжения на емкости заданной схемы. Для определения постоянных интегрирования других токов и напряжений необходимо найти изменение производных этих величин в моменты коммутации. Это приведет к усложнению и увеличению объема расчетов. Поэтому в этом методе целесообразно определить токи и напряжения на реактивных элементах, а затем, если это возможно, по законам Кирхгофа определить все другие токи и напряжения.
Запишем решение для тока i0(t) = iL(t) и его производной uL(t) =
= LdiL(t)/dt на интервалах в соответствии с выражениями (4) и (5).
Первый интервал [0+; T/2–]: u11 = U,
i01вын = U/R2, uL1вын = 0 — эти вынужденные значения получены из системы уравнений (3) для t = ¥ при условии, что u11 = сonst.
Второй интервал [T/2+; T–]: u12 = – U,
i02вын = –U/R2, uL2вын = 0.
Проведем сопряжение решений на интервалах для тока i0 и напряжения uL, используя значения разностей (6), (7):
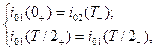
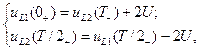
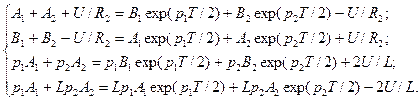(8)
Получили систему алгебраических уравнений (8) в общем виде с неизвестными постоянными интегрирования.
Расчет i0(t), uL(t) и выходного напряжения u2(t) проведем для значений параметров заданной схемы (см. рис. 18): R1 = 15 Ом,
= 1 Ом, 
= 4 Ом, L = (100/21) мГн, C = (5/21)×103 мкФ.
Для определения корней составим характеристическое уравнение: p2 + (R1R2C + L) / [(R1 + R2)LC] p + R2 / [(R1 + R2)LC] = 0. Введем обозначения d = (R1R2C + L) / [2(R1 + R2)LC] = 500,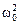 
= R2 /
/ [(R1 + R2)LC] = 21×104. Определим корни: p1,2 = – d ± (d2 - ) =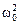
= –500 ± 200, p1 = – 300 с–1, p2 = – 700 с–1. Корни действительные, различные, отрицательные — процесс апериодический, т.е. записанные решения (4) и (5) в общем виде соответствуют этим корням.
Подставим в уравнения системы (8) значения корней и параметров схемы:
Решая эту систему относительно A1, A2, В1, В2 найдем A1 =
= 5,0365, A2 = –13,501, В1 = 5,0365, В2 = 13,501.
Теперь можем записать окончательное решение для i0(t), uL(t) на интервалах:
Напряжение u2(t) на выходе четырехполюсника найдем согласно закону Кирхгофа: u2(t) = (u1(t) – uL(t)) 
/R2 = 0,8[u1(t) – uL(t)]:
Для проверки результатов расчета из найденных решений определим значение разности напряжения uL(t) на границе первой коммутации: uL1 = [uL1(0+) – uL2(T–)] = 38,808 – (– 2,186) = 39,994 » » 40 В, что соответствует с достаточной точностью значению действительной разности (6) uL1 = 40 В.
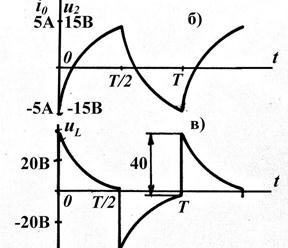
На рис. 18 с соблюдением масштаба построены графики u1(t), i0(t), u2(t) и uL(t).
Рис. 18
Дата добавления: 2015-04-16; просмотров: 70; Мы поможем в написании вашей работы!; Нарушение авторских прав |