Расчет четырехполюсника

Пример 3. Для схемы рис. 9 рассчитать токи и напряжения методом входного сопротивления, построить их векторные диаграммы. В схеме заданы: u _вх = 40 sin(10³t +p/2) B, R₁ = X_C1 =
= X_C2 = R₃ = X_L3 = 10 Ом.

Решение. Обозначим точки соединения элементов схемы и токи. Выберем условно положительные направления токов в соответствии с рис. 9. Ток в неразветвленной части схемы I₁ = U _вх / Z _вх, где Z _вх — комплексное входное сопротивление схемы, Z _вх = R₁ – jX_C1 + [–j X_C2(R₃ + j X_L3)] / [R₃ + j(X_L3 – X_C2)] = 10 –j10 + [–j10(10 + j10)] / [10 + j(10 –10)] = (20 – j20) Ом.

Комплексное действующее значение входного напряжения U_вх = j40 B. Общий ток I₁ = j40/(20 – j20) = –1 + j = exp135°. Токи в параллельных ветвях выразим через ток I₁: I₂ = I₁Z₃ / (Z₂ +
+ Z₃) = (–1 + j)(10 + j10) / (–j10 + 10 + j10) = – 2 = 2exp( jp), I₃ =
= I₁Z₂ / (Z₂ + Z₃) = (–1 + j)(–j10) / 10 = 1 + j = 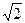exp( jp/4).

Построим векторную диаграмму — совокупность векторов токов или напряжений на комплексной плоскости с учетом их взаимной ориентации по фазе. Ток в неразветвленной части схемы равен геометрической сумме токов I ₁ = I ₂ + I ₃. Векторная диаграмма токов с учетом выбранного масштаба m_I = 0,5 A/см представлена на рис.10, а.

Для построения векторной диаграммы напряжений рассчитаем напряжения на отдельных элементах (участках) схемы
(см. рис. 9). Направления напряжений принимаем совпадающими с направлением токов в соответствующих элементах. Рассчитаем падение напряжения на элементах схемы: U_R1 = U_ed = R₁ I₁ =
= 10 и совпадает по фазе с током I₁; U_C1 = U_dc = X_C1 I₁ = 10 , но отстает по фазе от тока I₁ на угол p/2; U_R3 = U_cb = R₃I₃ =
= 10 и совпадает по фазе с током I₃; U_L3 = 14,1 и опережает по фазе ток I₃ на угол p/2; напряжение U_ca = X_C2 I₂ = 20 и отстает по фазе от тока I₂ на угол p/2.

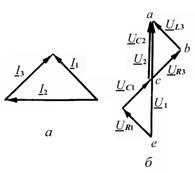
Рис. 9 Рис. 10

Геометрическая сумма U_R1 + U_C1 + U_R3 + U_L3 = U_вх = U_ea, а сумма U_R3 + U_L3 равна по модулю падению напряжения на емкости С₂ — U_ca. Кроме того, эта векторная сумма равна выходному напряжению четырехполюсника.

Векторная диаграмма напряжений показана на рис.10, б (m_U
= 8 B/см). Мгновенные значения тока i₁ и выходного напряжения u_вых: I₁ = exp( j3p /4) i₁ = 2 sin(10³t + 3p/4), U_вых = j20 u_вых
= 20 sin(10³t + p/2). Сдвиг по фазе между выходным и входным напряжениями j = y_вых – y_вх = p/2 – p/2 = 0, а отношение действующих значений U_вых / U_вх = 20/40 = 0,5.