Решение по первому и второму законам Кирхгофа
Расставляю произвольное положительное направление искомых токов в ветвях и обозначаю их на схеме , показанной на рисунке 2. Ветвь с условным обозначением вольтметра не участвует в измерениях из-за очень малых токов.
I3 
| 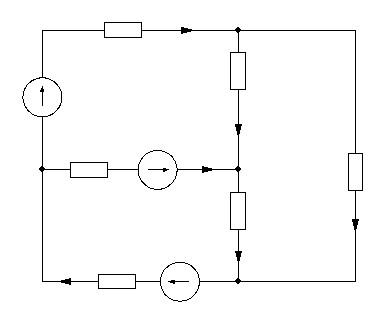
Рисунок 2 - Схема электрическая принципиальная расчетной цепи
В итоге на схеме, рисунок 2, остаётся четыре узла, так как узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка, то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом.
Рассчитываю количество уравнений по первому и второму закону Кирхгофа.
у= 4 – число узлов;
в= 6 – число ветвей;
вит= 0 – число ветвей с источником тока.
Количество уравнений по первому закону Кирхгофа n1 = у −1 = 3
Количество уравнений по второму закону Кирхгофа n2 = в − вит −(у − 1) = 3
Согласно первому заданию составляю системы уравнений по первому и второму законам Кирхгофа. По 1-му закону Кирхгофа для (у-1) узлов схемы, с учетом токов от источников тока, где y – число узлов схемы. Уравнение для последнего узла не составляют, т.к. оно совпало бы с уравнением, полученным при суммировании уже составленных уравнений для предыдущих узлов (т.е. линейно-независимых уравнений – (y-1)). При составлении уравнений следуют правилу: если ток выходит из узла, то его записывают со знаком «–», если входит – то со знаком «+».
Уравнения по первому закону Кирхгофа:
1) I2 – I1 – I3 = 0 (по 1 точке)
2) I1 – I4 – I5 = 0 (по 2 точке)
3) I3 + I4 – I6 = 0 (по 3 точке)
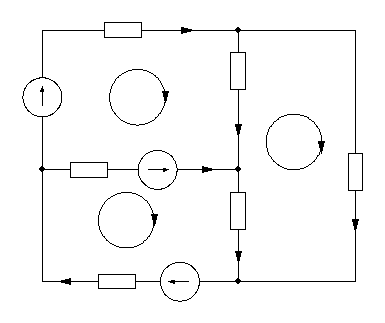
Для составления уравнений по второму закону Кирхгофа, используется нарисованная схема, показанная на рисунке 3.
Рисунок 3 - Схема электрическая принципиальная расчетной цепи
Уравнения по второму закону Кирхгофа:
I. I1R1 – I3R3 + I4R4 = E1 – E2
II. I5R5 – I4R4 – I6R6 = 0
III. I2R2 + I6R6 + I2R2 = E2 + E3
|


