
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение методом узловых потенциалов
| I1 |
| R4 |
| R1 |
| I1 |
| I2 |
| R1 |
| R2 |
| R3 |
| E1 |
| E2 |
| I4 |
| I3 |
| R4 |
| R5 |
| I5 |
| E3 |
| I6 |
| R6 |
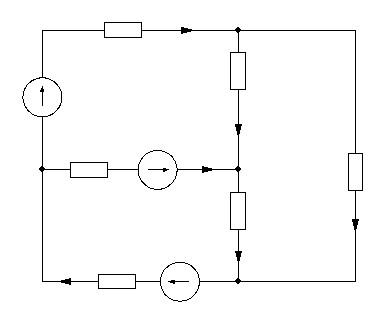
Рисунок 6 – Схема электрическая принципиальная расчетной цепи
Рассчитывают количество уравнений по первому и второму закону Кирхгофа.
Количество уравнений по первому закону Кирхгофа:
n1 = у −1 = 3
Количество уравнений по второму закону Кирхгофа:
n2 = в −вит −(у −1) = (6 – 0) – (4 – 1) = 3
Принимают потенциал одного из узлов равным 0.
Составляют уравнение для каждого из оставшихся (y-1) узлов согласно правилам:
1) левая часть уравнения равна сумме произведений потенциала рассматриваемого узла на сумму проводимостей всех ветвей, сходящихся в этом узле, взятое со знаком плюс, и потенциалов остальных узлов на сумму проводимостей ветвей, соединяющих эти узлы с рассматриваемым узлом, взятые со знаком минус;
2) правая часть уравнения равна алгебраической сумме произведений ЭДС ветвей, сходящихся в рассматриваемом узле на проводимости этих ветвей (так называемый узловой ток рассматриваемого узла). При этом произведения берутся со знаком плюс, если ЭДС направлены к рассматриваемому узлу.
Примечание
При наличии ветвей с источником тока необходимо учесть следующее:
1) проводимость ветви с источником тока равна нулю;
2) в правую часть уравнения добавляется алгебраическая сумма токов от источников тока в ветвях, сходящихся в рассматриваемом узле. При этом ток источника тока берется со знаком плюс, если он направлен к рассматриваемому узлу.
Уравнения:
1) φ1*(1/R1+1/R2+1/R3) – φ2*1/R1 – φ3*1/R3 = E3*1/R2–E2*1/R3–E1*1/R1
2) φ2*(1/R1+1/R4+1/R5) – φ1*1/R1 – φ3*1/R4 = E1*1/R1
3) φ3*(1/R3+1/R4+1/R6) – φ1*1/R3 – φ2*1/R4 = E2*1/R3
Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), имеющих общий узел, этот общий узел принимают за опорный узел (заземляют). Тогда потенциалы узлов, соединенных этими идеальными источниками ЭДС без пассивных элементов с опорным узлом, равны ЭДС этих идеальных источников (–E, если идеальный источник ЭДС направлен от опорного узла и +E в противном случае).
Определяем величину и направление токов в ветвях по закону Ома для участка цепи, содержащего ЭДС.
Закон Ома для участка цепи:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи: I=U/R.
I – величина тока, протекающего через участок цепи;
U – величина приложенного напряжения к участку цепи;
R – величина сопротивления рассматриваемого участка цепи.

| φ2 |
| R1 |
| φ1 |
| I1 |
| U12 |
| E1 |
Рисунок 7 – Схема электрической ветви для расчета тока I1
1) Составляю уравнение по ветке, показанной на рисунке 7.

Так как E1 направлено по направлению тока в цепи, то записывается в формуле со знаком плюс.
2)
| φ1 |
 Составляю уравнение по ветке, показанной на рисунке 8.
Составляю уравнение по ветке, показанной на рисунке 8.
| R2 |
| φ0 |
| I2 |
| U01 |
| E3 |
Рисунок 8 – Схема электрической ветви для расчета тока I2
Уравнение для I2:

Так как E3 направлено по направлению тока в цепи, то записывается в формуле со знаком плюс.
3)
| φ3 |
 Составляю уравнение по ветке, показанной на рисунке 9.
Составляю уравнение по ветке, показанной на рисунке 9.
| R3 |
| φ1 |
| I3 |
| U13 |
| E2 |
Рисунок 9 – Схема электрической ветви для расчета тока I3
Уравнение для I3:

Так как E2 направлено по направлению тока в цепи, то записывается в формуле со знаком плюс.
4) Составляю уравнение по ветке, показанной на рисунке 10.
| I4 |
| φ3 |
| U23 |
| R4 |
| φ2 |
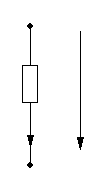
Рисунок 10 – Схема электрической ветви для расчета тока I4
Уравнение для I4:

Так как I4 направлено в том же направлении, как и U23,то напряжение записывается в формуле со знаком плюс.
5) Составляю уравнение по ветке, показанной на рисунке 11.
| I5 |
| φ2 |
| φ0 |
| U20 |
| R5 |

Рисунок 11 – Схема электрической ветви для расчета тока I5
Уравнение для I5:

Так как φ0 равно нулю, то φ0 сокращается
6) Составляю уравнение по ветке, показанной на рисунке 12.
| φ3 |
| φ0 |
| I6 |
| U30 |
| R6 |

Рисунок 12 – Схема электрической ветви для расчета тока I6
Уравнение для I6:

Так как φ0 равно нулю, то φ0 сокращается.
Дата добавления: 2015-04-16; просмотров: 336; Мы поможем в написании вашей работы!; Нарушение авторских прав |