Методы анализа цепей

Анализ или расчет цепи заключается в определении значений токов, напряжений и мощностей отдельных участков, если заданы параметры схемы замещения цепи. Методы расчета цепей базируются на применении законов Кирхгофа.

Рассмотрим некоторую электрическую цепь, которая содержит n_У узлови n_В ветвей, в том числе n_T ветвей с источниками тока. Электрический режим цепи будет полностью определен, если будут найдены токи во всех ветвях. Если расчет электрической цепи производить путем непосредственного применения законов Кирхгофа, то необходимо составить систему n_В – n_T уравнений и решить ее. При этом число независимых уравнений, составленных по первому закону Кирхгофа, будет равно n_У – 1, т. е. на единицу меньше числа узлов. Остальные уравнения в количестве n = n_В – ( n_У – 1) – n_T составляются по второму закону Кирхгофа для независимых контуров.

Так как направления токов в ветвях сложной электрической цепи заранее неизвестны (за исключением ветвей с источниками токов), то предварительно выбирают их положительные направления. Контуры следует выбирать так, чтобы в них вошли все ветви схемы, а в каждый из контуров возможно меньшее число ветвей. Контуры взаимно независимы, если каждый последующий контур, для которого составляется уравнение, имеет не менее одной новой ветви.

Пример 1. Найти токи ветвей и напряжение U_Jна зажимах источника тока цепи, схема которой приведена на рисунке 1, методом непосредственного применения законов Кирхгофа. Параметры элементов схемы: E₄ = = 6 B, E₅ = 4 B, J = 3 А, R₁ = 2 Ом, R₂ = 4 Ом, R₃ = 5 Ом, R₄ = 3 Ом, R₅ = 4 Ом.

Решение. Укажем стрелками произвольно выбранныенаправления токов в ветвях схемы и соответствующие им падения напряжений на сопротивлениях. Обозначим узлы буквами a, b, c и d. Имеем n_В= 6, n_T = 1, n_У = 4. Составим систему уравнений в количестве n_В – n_T = 5для определения неизвестных токов. В соответствии с первым законом Кирхгофа составим три уравнения для узлов a ,b и c:

I₁ + I₃ – J = 0;

– I₁ + I₂ + I₄ = 0;

– I₂ + I₅ + J = 0.

По второму закону Кирхгофа необходимо записать два уравнения, для чего выберем два независимых контура I и II c указанными стрелками направлениями их обхода.

U₁ + U₄ – U₃ = E₄;

U₂ + U₅ – U₄ = E₅ – E₄,

где U₁ = R₁I₁, U₂ = R₂I₂, U₃ = R₃I₃, U₄ = R₄I₄, U₅ = R₅I₅.

Подставив числовые значения заданных параметров схемы, получим систему уравнений:

I₁ + I₃ = 3;

3. I₁ + I₂ + I₄ = 0;

I₂ + I₅ = – 3;

2I₁ – 5I₃ + 3I₄ = 6;

4I₂ – 3I₄ + 4I₅ = –2,

Решая которую, находим искомые токи:

I₁ = 2,584 А; I₂ = 1,614 А; I₃ = 0,416 А; I₄ = 0,97 А; I₅ = –1,386 А.

Ток I₅ имеет отрицательный знак, это означает, что его действительное направление противоположно предварительно выбранному.

Пример 2. Для электрической цепи рис. 2 записать уравнения по законам Кирхгофа.

Электрическая цепь содержит 6 ветвей, 3 узла. Направления токов в ветвях выбрано произвольными. Всего требуется записать 6 независимых уравнений для определения токов во всех ветвях. Для двух любых узлов, например, 1 и 3, по первому закону Кирхгофа составляем два уравнения. Втекающие в узел токи возьмем со знаком плюс.

Для узла 1: –I₁ + I₂ – I₃ – I₅ + I₆ = 0.

Для узла 3: –I₄ + I₅ – I₆ = 0.

По второму закону Кирхгофа для 4 независимых контуров запишем уравнения. Направление обхода контуров выберем по часовой стрелке. В электрической цепи можно выделить 4 независимых контура, например: 1-й контур – E₁ – R₁ – R₂ – R₃, 2-й контур – R₃ – R₄ – E₂, 3-й контур – E₂ – R₄ – R₅ – E₃ – R₂, 4-й контур – R₇ – E₄ – R₆.

Для 1 – го контура: (R₁ + R₂) ∙ I₁ + R₃ ∙ I₂ = E₁.

Для 2 – го контура: – R₃ ∙ I₂ – R₃ ∙ I₃ = E₂.

Для 3 – го контура: R₄ ∙ I₃ – R₅ ∙ I₄ – R₇ ∙ I₅ = – E₂ + E₃.

Для 4 – го контура: R₇ ∙ I₅ + R₆ ∙ I₆ = E₄

При вычислении токов в ветвях электрической цепи удобнее пользоваться матричной формой записи уравнений Кирхгофа:

A ∙ I = B ∙ E, (3)

где A,B – квадратные матрицы коэффициентов при токах и напряжениях порядка b×b; I,E – матрицы – столбцы неизвестных токов и заданных ЭДС.

Элементами матрицы А являются коэффициенты при токах в левой части уравнений, составленных по первому и второму законам Кирхгофа. Первые y – 1 строк матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, –1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.

Элементы следующих b – y + 1строк матрицы А равны значениям сопротивлений при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком.

Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые y – 1 строк матрицы имеют нулевые элементы, так как ЭДС в правой части уравнений, записанных по первому закону Кирхгофа, отсутствуют. Остальные b – y + 1 строки содержат элементы +1, –1 в зависимости от того, с каким знаком входит ЭДС в уравнение, и 0, если ЭДС в уравнение не входит.

Общее решение уравнений, составленных по законам Кирхгофа:

I = (A^-1B)∙E = GE (4)

где G = A^-1B – матрица проводимостей;

(5)

Токи в каждой ветви:

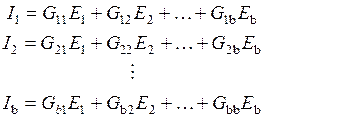(6)

Пример3.Для схемы рис. 2 записать уравнения по законам Кирхгофа в матричной форме записи. По первому закону Кирхгофа составлены два уравнения для узлов 1 и 3

– I₁ + I₂ – I₃ – I₅ + I₆ = 0; – I₄ + I₅ – I₆ = 0.

По второму закону Кирхгофа записываются 4 уравнения для контуров

(R₁ + R₂) ∙ I₁ + R₃ ∙ I₂ = E₁; – R₃ ∙ I₂ – R₃ ∙ I₃ = E₂; R₄ ∙ I₃ – R₅ ∙ I₄ – R₇ ∙ I₅ = – E₂ + E₃; R₇ ∙ I₅ + R₆ ∙ I₆ = E₄

В матричной форме записи

A ∙ I = B ∙ E,

где

; ;

; .