МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ

Этот метод базируется на применении первого закона Кирхгофа и закона Ома. Суть метода заключается в том, что расчетным путем определяются потенциалы узлов электрической схемы относительно какого-либо узла, принятого в качестве базисного, а потенциал последнего принимают равным нулю. Расчет сводится к решению системы m = n_у – 1 уравнений, составленных только по первому закону Кирхгофа. Решив систему уравнений, находят потенциалы узлов, а затем по закону Ома определяют токи ветвей, соединяющих узлы.

Для определения потенциалов (φ₁, φ₂, …, φ_k, …, φ_m) узлов электрической схемы составляется следующая система уравнений:

G₁₁φ₁ – G₁₂φ₂ –… – G_1kφ_k – … – G_1mφ_m =

– G₂₁φ₁ + G₂₂φ₂ – … – G_2kφ_k – … – G_2mφ_m =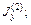

……………………………………………….. (11)

– G_k1φ₁ – G_k2φ₂ + … + G_kkφ_k – … – G_kmφ_m =

…………………………………………………

– G_m1φ₁ – G_m2φ₂ – … – G_mkφ_k – … + G_mmφ_m =

где G_kk – собственная проводимость узла k, равная сумме проводимостей

ветвей, соединенных с этим узлом; эта проводимость всегда по-

ложительна;

G_km – взаимная проводимость между узлами k и m, равная сумме прово-

димостей ветвей, непосредственно соединяющих эти узлы; взаим-

ную проводимость всегда берут со знаком ”минус“, при этом

G_km = G_mk;

– узловой ток k-го узла, состоящий из слагаемых:

– алгебраическая сумма произведений ЭДС ветвей, присоединен-

ных к узлу k,на их проводимости; при этом со знаком ”плюс“

берутся те ЭДС, которые действуют в направлении узла k, а

со знаком ”минус“ – в направлении от узла k;

– алгебраическая сумма токов источников тока, присоединенных к

узлу k; эти токи берутся со знаком ”плюс“, если они направлены к

узлу k, и со знаком ”минус“ при их направлении от узла k.

Система уравнений узловых потенциалов (12) может быть записана в матричной форме

(12)

где

Решив уравнение (12) относительно матрицы получим

(13)