Порядок расчета. 1. Произвольно выбрать положительные направления токов в ветвях исходной схемы.

1. Произвольно выбрать положительные направления токов в ветвях исходной схемы.

2. Произвольно выбрать положительные направления контурных токов для каждого независимого контура электрической схемы. Если в схеме есть ветви с источниками тока, то сначала выбирают контурные токи таким образом, чтобы каждый из них проходил по ветви с источником тока и совпадал с ним по направлению. Таким образом, эти контурные токи J_i будут заранее известны. Остальные контурные токи выбирают проходящими по ветвям, не содержащим источников тока.

3. Обходя каждый из независимых контуров в выбранном направлении, записать n линейных алгебраических уравнений следующего вида:

R₁₁I₁₁ + R₁₂I₂₂ + … + R_1kI_kk + … + R_1nI_nn + = E_11;

… …

R_k1I₁₁ + R_k2I₂₂ + … + R_kkI_kk + … + R_knI_nn + = E_kk; (7)

… …

R_n1I₁₁ + R_n2I₂₂ + … + R_nkI_kk + … + R_nnI_nn + = E_nn,

где R_kk – собственное сопротивление контура k, равное сумме сопротивлений всех ветвей контура k; значения R_kk всегда записывают со знаком “плюс”; R_kn – общее сопротивление контуров k и n, причем, R_kn = R_nk; общее сопротивление контуров записывается со знаком “плюс”, если контурный ток I_kk совпадает по направлению с контурным током I_nn, в противном случае оно записывается со знаком “минус”; _ki – общее сопротивление контура k и контура I, по которому циркулирует ток источника тока J_i; знак R_ki выбирают по тем же правилам, что и сопротивления R_kn; E_kk – контурная ЭДС, равная алгебраической сумме ЭДС контура k; ЭДС, действующие в направлении обхода контура, берут со знаком „плюс“, а направленные встречно – со знаком “минус”.

4. Вычислить истинные токи в ветвях в виде алгебраических сумм контурных токов, протекающих по соответствующим ветвям.

Пример 4. Рассчитать методом контурных токов токи в цепи, схема которой приведена на рисунке 1.

Дано: E₁ = 50 B, E₄ = 150 B, E₅ = 30 B, J = 3 А, R₁ = 10 Ом, R₂ = 15 Ом, R₃ = 5 Ом, R₄ = 5 Ом, R₅ = 25 Ом.

Решение. Выберем положительные направления токов ветвей и укажем их на схеме стрелками. Схема содержит три независимых контура, в одном из которых контурный ток выберем равным току источника тока J. Два других контурных тока обозначим I₁₁ и I₂₂ соответственно и укажем их направление. Составим систему линейных алгебраических уравнений в соответствии с (7).

R₁₁I₁₁ + R₁₂I₂₂ + R₁₃ J = E_11;

R₂₁I₁₁ + R₂₂I₂₂ + R₂₃ J = E_22,

где R₁₁ = R₁ + R₂ + R₃ = 30 Ом; R₂₂ = R₂ + R₄ + R₅ = 45 Ом; R₁₂ = R₂₁ = R₂ = 15 Ом;

R₁₃ = – R₃ = 5 Ом; R₂₃ = R₅ = 25 Ом; E₁₁ = E₁ = 50В; E₂₂ = E₄ – E₅ = 120 В.

Подставим числовые значения и получим систему уравнений

30I₁₁ + 15I₂₂ = 65;

15I₁₁ + 45I₂₂ = 45,

решив которую найдем контурные токи I₁₁ = 2 А, I₂₂ = 0,333 А.

Токи в ветвях равны алгебраической сумме контурных токов, проходящих по этим ветвям:

I₁ = I₁₁ = 2 А; I₂ = I₁₁ + I₂₂ = 2,333 А; I₃ = – I₁₁ + J = 1 A; I₄ = I₂₂ = 0,333 А;

I₅ = – I₂₂ – J = – 3,333 A.

Ток I₅ имеет направление, противоположное выбранному.

Пример 5. Записать уравнения по методу контурных токов для схемы рис. 5.

Схема содержит шесть ветвей (b = 6) с неизвестными токами и три узла (y = 3). Так как k = b – y + 1 = 4, то предпочтителен метод контурных токов. Для четырех контуров с токами I_k1, I_k2, I_k3, I_k4 записывают уравнения по второму закону Кирхгофа:

(8)

где R₁₁ = R₁ + R₂ + R₃, R₂₂ = R₃ + R₄, R₃₃ = R₄ + R₅ + R₇, R₄₄ = R₆ + R₇ – полное сопротивление соответствующих контуров; R₁₂ = R₂₁ = R₃, R₂₃ = R₃₂ = R₄, R₃₄ = R₄₃ = R₇ – сопротивление ветвей связи первого контура со вторым R₁₂, второго с первым R₂₁ и так далее E₁₁ = E₁, E₂₂ = E₂, E₃₃ = – E₂ + E₃, E₄₄ = E₄ – полные ЭДС контуров.

Токи ветвей (смотри их обозначение на рис. 5) определяются по первому закону Кирхгофа. Например, в ветви с сопротивлениями R₁, R₂ протекающий снизу вверх ток I₁ равен контурному току I₁ = I_k1, в ветви с сопротивлением R₃ протекающий сверху вниз ток равен разности токов

I₂ = I_k1 – I_k2, I₃ = – I_k2 + I_k3, I₄ = – I_k3, I₅ = – I_k3 + I_k4, I₆ = – I_k4.

Если в электрической цепи будет иметься n независимых контуров, то количество уравнений будет равно n.

Общее решение системы n уравнений относительно тока I_kk

. (9)

Здесь 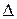– определитель системы.

(10)

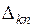– есть алгебраическое дополнение, полученное из определителя 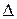путем вычеркивания k столбца и n строки и умножения полученного определителя на (–1)^{k + n}.

В матричной форме записи уравнение (10) имеет вид R_k∙I_k = E_k; I_k = G_k∙E_k = R_k^–1∙E_k и являются общей матричной формой записи и решения уравнений по методу контурных токов.

Контуры и направления контурных токов в них показаны на схеме рис. 5.

Контур с известным контурным током J проведем по ветви с элементами R₅, Е₅. Система уравнений для контурных токов I₁₁, I₂₂ и I₃₃ имеет вид:

(R₁ + R₃ + R₆ )I₁₁ – R₁ I₂₂ – R₃ I₃₃ = – E₁ + E₃

5. R₁ I₁₁ + (R₁ + R₂ + R₄) I₂₂ – R₄ I₃₃ = E₁ + E₂ – E₄

– R₃ I₁₁ – R₄ I₂₂ + (R₃ + R₄ + R₅) I₃₃ – R₅ J = – E₃ + E₄ + E₅

Подставив известные числовые значения, получим:

13 I₁₁ – 5 I₂₂ – 4 I₃₃ = – 2

–5 I₁₁ + 14 I₂₂ – 5 I₃₃ = 32

6. 4 I₁₁ – 5 I₂₂ +12 I₃₃ = 52

Откуда значения контурных токов: I₁₁ = 5,7 А, I₂₂ = 7,7 А, I₃₃ = 9,45 А.

Определим токи в ветвях: I₁ = – I₁₁ + I₂₂ = 2 А , I₂ = I₂₂ = 7,7 А,

I₃ = I₁₁ – I₃₃ = –3,75 А, I₄ = I₂₂ – I₃₃ = – 1,75 А, I₅ = I₃₃ – J = 5,45 А, I₆ = I₁₁ = 5,7 А.

Если токи рассчитаны методом контурных токов, то первый закон Кирхгофа для всех узлов цепи выполняется автоматически. Чтобы убедиться в том, что токи найдены верно, проверим тождественность уравнений, составленных по второму закону Кирхгофа для контуров I, II и III, подставив в них числовые значения:

,

,

.

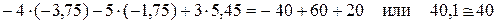Пример 6. Рассчитать токи в схеме на рисунке 3 с параметрами E₁ = 12 В, E₅ = 8 В, J = 2 A, r₀₁ = 1 Ом, r₀₅ = 1,2 Ом, R₁ = 11 Ом, R₂ = 8 Ом, R₃ = 14 Ом, R₄ = 5 Ом, R₅ = 6,8 Ом, R₆ = 6 Ом методом контурных токов. Построить потенциальную диаграмму для контура a-b-c-d-a.

Решение. Подключим источник тока J параллельно сопротивлениям R₂ и R₄ (рис. 6, а), распределение токов в узлах a, b и c при этом останется прежним. Заменим параллельное соединение источников тока J и сопротивлений R₂ и R₄ эквивалентным последовательным соединением ЭДС Е₂ = R₂J = 16 В и Е₄ = R₄J = 10 В с соответствующими сопротивлениями R₂ и R₄ (рис. 6., б).

В результате эквивалентных преобразований получим схему на рис. 6 Токи в ветвях с сопротивлениями R₂ и R₄ этой схемы будут отличаться от токов в исходной схеме, поэтому обозначим их и .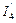

Выберем независимые контуры и направим в них контурные токи I₁₁, I₂₂ и I₃₃. Запишем систему уравнений относительно неизвестных контурных токов в матричной форме и найдем ее решение.

,

где R₁₁ = R₁ + r₀₁ + R₂ + R₃ = 34 Ом;

R₂₂ = R₂ + R₄ + r₀₅ + R₅ = 21 Ом;

R₃₃ = R₃ + R₆ + r₀₅ + R₅ = 28 Ом;

R₁₂ = R₂₁ = – R₂ = – 8 Ом;

R₁₃ = R₃₁ = R₃ = 14 Ом;

R₂₃ = R₃₂ = r₀₅ + R₅ = 8 Ом;

E₁₁ = E₁ – E₂ = – 4 В;

E₂₂ = E₂ + E₄ – E₅ = 18 В;

E₃₃ = – E₅ = – 8 В.

Решение системы линейных алгебраических уравнений выполним методом Крамера. Найдем определитель матрицы сопротивлений

1,012∙10⁴ Ом³,

а также следующие определители:

Находим контурные токи:

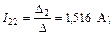
Токи ветвей схемы 4:

I₁ = I₁₁ = 0,674 A; = – I₁₁ + I₂₂ = 0,842 A; I₃ = – I₁₁ – I₃₃ = 0,382 A;

= I₂₂ = 1,516 A; I₅ = – I₂₂ – I₃₃ = – 0,46 A; I₆ = – I₃₃ = 1,056 A.

Вернемся к исходной схеме и определим токи во второй и четвертой ветвях по первому закону Кирхгофа:

I₂ = I₃ – I₅ – J = – 1,158 А; I₄ = I₁ + I₂ = – 0,484 А.

Проверим правильность результатов расчета по балансу электрических мощностей. Найдем напряжение U_J на зажимах источника тока:

U_J = – R₂I₂ – R₄I₄ = 11,684 В.

Истинные направления токов I₂ и I₄ противоположны предварительно выбранным.